meta data for this page
Gruppe 346: Der kippende Besenstiel
Der Versuch wurde durchgeführt von: Elisheva Naor und Johanna Giesbrecht
Die Wiki-Seite wurde angelegt am: 7 January 2021 14:27
Messungen
Wir beginnen die Messung, indem wir den Besenstiel auf einem Teppich an ein Bücherregal stellen und dabei festhalten. Lassen wir den Besenstiel los, fällt er; das ist unsere Messung für den Startwinkel Null. Um die variierten Startwinkel messen zu können, kippen wir den Besenstiel zur Seite, messen möglichst waagerecht den Abstand von der Spitze zum Regal und berechnen über den ArcusSinus den Winkel im Bogenmaß.
1. Besenstiel, 130 cm:
1. Winkel: 0 (0 cm)
- 1.429
- 1.428
- 1.398
- 1.429
- 1.519
- → 1.441 +/- 0.078
2. Winkel: 0.077 (10 cm)
- 0.755
- 0.871
- 0.981
- 0.781
- 0.803
- → 0.838 + 0.143
4. Winkel: 0.313 (40 cm)
- 0.643
- 0.619
- 0.475
- 0.601
- 0.626
- → 0.593 + 0.118
5. Winkel: 0.569 (70 cm)
- 0.403
- 0.471
- 0.301
- 0.430
- 0.420
- → 0.405 + 0.104
6. Winkel: 0.878 (100 cm)
- 0.101
- 0.256
- 0.245
- 0.296
- 0.292
- → 0.238 + 0.137
2. Besenstiel: 0.88 cm
1. Winkel: 0 (0 cm)
- 1.298
- 1.348
- 1.244
- 1.349
- 1.113
- → 1.270 + 0.157
2. Winkel: 0.114 (10 cm)
- 0.687
- 0.692
- 0.812
- 0.663
- 0.553
- → 0.681 + 0.131
3. Winkel: 0.288 (25 cm)
- 0.560
- 0.534
- 0.430
- 0.502
- 0.543
- → 0.514 + 0.084
4. Winkel: 0.472 (40 cm)
- 0.309
- 0.464
- 0.381
- 0.362
- 0.379
- → 0.379 + 0.085
5. Winkel: 1.020 (75 cm)
- 0.145
- 0.200
- 0.186
- 0.211
- 0.150
- → 0.178 + 0.033
2. Besenstiel mit Luftreibung
1. Winkel: 0.114 (10 cm)
- 0.884
- 0.9
- 0.787
- 0.779
- 0.789
- → 0.828 + 0.072
2. Winkel: 0.288 (25cm)
- 0.715
- 0.683
- 0.599
- 0.690
- 0.602
- → 0.658 + 0.057
3. Winkel: 0.472 (40cm)
- 0.599
- 0.415
- 0.469
- 0.506
- 0.553
- → 0.508 + 0.093
4. Winkel:1.020 (75cm)
- 0.479
- 0.511
- 0.322
- 0.311
- 0.361
- → 0.397 + 0.114
Numerische Lösung
Das Verfahren zur Bestimmung einer numerischen Lösung der Differentialgleichung ist ein Iterationsverfahren. Für die erste Iteration nehmen wir logischerweise an, der Winkel zu Beginn der Messung sei 0. Damit kommen wir über die DGL direkt auf die Beschleunigung zu Beginn der Messung.
Für hinreichend kleine Zeitintervalle dt können wir auf jedem dieser Intervalle eine lineare Bewegung annehmen; Wir definieren also die Geschwindigkeit nach dt als die Startgeschwindigkeit (hier ebenfalls 0) plus die Anfangsbeschleunigung mal das Zeitintervall dt. Analog können wir den zurückgelegten Winkel nach dt berechnen.
Für weitere Iterationen verwenden wir nicht mehr die Startbeschleunigung, sondern die Beschleunigung aus der vorangegangenen Iteration, so auch mit der Geschwindigkeit.
Der Endwinkel, bei dem das Verfahren endet, ist Pi/2, also 90°, dann liegt der Stab auf dem Boden.
Daher beenden wir die Iteration durch eine While-Schleife, sobald ein Winkel von etwa Pi/2 erreicht ist. Die Fallzeit erhalten wir über n*dt, also die Iterationsanzahl mal die Zeiteinheit, in unserem Fall 0,01 s.
Für das Programmieren einer solchen Iteration haben wir die Programmiersprache Python verwendet. Dabei haben wir den Winkel phi und die Winkelgeschwindigkeit v mit Hilfe von For-Schleifen definiert, wobei i der Laufindex im Bereich 0 bis n bzw. 0 bis n+1 ist. a ist die Winkelbeschleunigung, die durch die DGL gegeben wird.
Mit Hilfe einer While-Schleife begrenzen wir das Verfahren auf einen maximalen Winkel von Pi/2, da der Stab weiter nicht fallen kann.
Als Parameter können die Zeitspanne dt und insbesondere der Startwinkel Phi0 variiert werden.
Ausgegeben wird der Endwinkel Phi, also die eigentliche numerische Lösung der DGL sowie die Fallzeit n*dt.
- hello-besenstiel-world.py
import math import sys def fv(v0, a, n, dt): v=v0 for i in range(0, n): v=v+a*dt return v def fPhi(Phi0, v0, n, dt): Phi=Phi0 for i in range(0, n+1): a=fa(Phi) v=fv(v0, a, i, dt) Phi=Phi+v*dt return Phi def fa(Phi): a=math.sin(Phi)/0.314**2 return a dt=0.01 Phi0=float(sys.argv[1]) v0=0 n=0 Phi=fPhi(Phi0, v0, n, dt) while(Phi<math.pi/2): print(n, "=>", Phi, "--- t=", n*dt, "s") n+=1 Phi=fPhi(Phi0, v0, n, dt) print(math.pi/2)
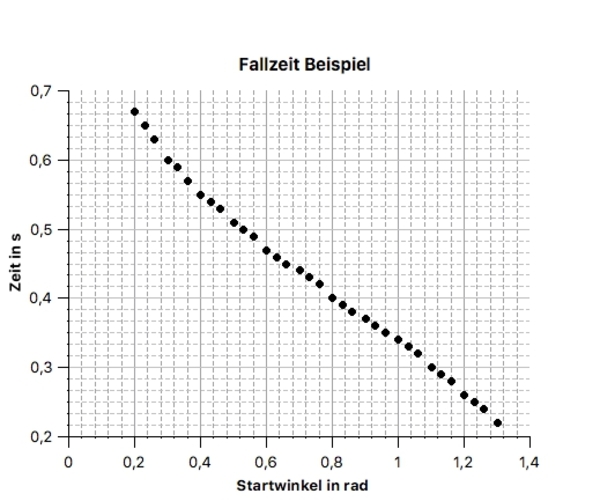
Zur Überprüfung unseres Programmes Vergleichen wir die Ausgabe mit dem Beispiel in der Versuchsanleitung für die gleichen Parameter. Bis auf eine unterschiedliche Skalierung der Achsen stimmen die Diagramme nahezu überein:
Die folgende Tabelle zeigt den Einfluss der Länge der Zeitintervalle auf die Fallzeit:
| dt | Fallzeit |
|---|---|
| 0,0005 | 0,6045 |
| 0,0009 | 0,6048 |
| 0,001 | 0,604 |
| 0,0015 | 0,6045 |
| 0,005 | 0,6 |
| 0,01 | 0,6 |
| 0,05 | 0,6 |
| 0,1 | 0,6 |
| 0,2 | 0,6 |
Erwartungsgemäß ist die Angabe der Fallzeit genauer, je kleiner man die Zeitintervalle wählt. Ab einem Zeitintervall von etwa 0,005 s bleibt die Fallzeit bei 0,6 s.
Syntax und Funktionen im Wiki
Hier noch Links zu