meta data for this page
Besenstiel -- Gruppe 326
Der Versuch wurde durchgeführt von: Jan Schimansky und Davin Höllmann
Die Wiki-Seite wurde angelegt am: 17 December 2020 21:09
Einleitung
Im folgenden Versuch wird die Kippbewegung eines Besenstiels und die damit verbundene Physik untersucht. Der Versuch ist in zwei Teile aufgeteilt. Zum einen wird im Home-Lab eine Messreihe von zwei kippenden Besenstielen aufgenommen. Untersucht werden verschiedene Startwinkel unter zwei verschiedenen Stablängen $l$ um die Kippzeit $T$ zu variieren. Zusätzlich wird ein kurzes Computerprogramm in Mathematica geschrieben, welches mithilfe des Zeitschrittverfahrens eine numerische Lösung für die Winkelbeschleunigung des Besens ausgibt. Die gegebene Differentialgleichung lautet: \begin{align} \ddot{\varphi}&=\frac{sin(\varphi)}{\tau^2}\\ \tau&=\sqrt{\frac{2*l}{3*g}} \end{align}
Im Wiki werden die Vorüberlegungen, der Computercode und der Versuchsaufbau sowie deren Messwerte dokumentiert. Der Versuchsbericht deckt dann die Auswertung und Erklärung des Beobachteten ab.
Vorüberlegungen
Beschreiben Sie die Kippbewegung mithilfe physikalischer Begriffe
Der Schwerpunkt des Stabes liegt in der Stabmitte wenn man annimmt, dass die Masse des Stabes homogen verteilt ist. Die Bewegung des Stabes verläuft nun in einer Drehbewegung um den Kontaktpunkt, also den Punkt auf dem der Stab steht, herum. Auf den Stab wirkt das Moment $\vec{M}=\vec{F}\times \vec{a}$, dieses Moment setzt sich aus dem Hebel $\vec{a}=sin(\varphi)\cdot \vec{L}\cdot \frac{1}{2}$ und der Kraft $\vec{F}=m\cdot \vec{g}$ zusammen. Für das Moment ergibt sich also $\vec{M}=(sin(\varphi)\cdot \vec{L}\cdot \frac{1}{2})\times (m\cdot \vec{g})$. Somit ist das Moment vom Hebel abhängig, dieser Hebel wird im Verlaufe der Kippbewegung immer größer, also wird auch das Moment und auch damit die Beschleunigung größer.
Begründen Sie: Vernachlässigt man die Luftreibung, so hängt bei gleicher Stablänge die Kippzeit $T$ nicht von der Stabmasse $m$ ab.
Analog zum freien Fall spielt bei der Kippbewegung die Masse des Besenstiels keine Rolle da unabhängig von ihrer Masse dieselbe Beschleunigung g auf sie wirkt. Neben der Gewichtskraft ist nach dem zweiten Newtonschen Gesetz die Beschleunigung proportional zur einwirkenden Kraft. \begin{align} F&=m\cdot a , F_G=m\cdot g\\ a&=\frac{F}{m}=\frac{F_G}{m}=\frac{m\cdot g}{m}=g\\ a&=g \end{align} Bei der Kippbewegung erfahren alle Stäbe der gleichen Form - unabhängig von ihrer Masse - dieselbe Beschleunigung a.
Alltägliche Erfahrung: Je kleiner der Anfangswinkel ist, desto größer ist die Kippzeit $T$
Je größer der Anfangswinkel desto geringer ist die Strecke die der Stab kippt und damit ist auch die Kippzeit geringer. Alltagserfahrung: Prokrastinieren beim Laub harken.
Welchen Einfluss hat die Stablänge?
Ein längerer Stab führt zu einer längeren Kippzeit. Dies liegt an der Abhängigkeit der Kippzeit vom Drehmoment $M=F\cdot a$ wobei der Hebel a länger ist, je länger der Stab ist.
Welche Schlussfolgerungen ergeben sich aus diesen Experimenten für das Jonglieren? Wie sollte der Stab beschaffen sein, damit das Jonglieren möglichst leicht gelingt?
Um den Stab gut Jonglieren zu können sollte die Zeit die man hat zwischen der der Stab zur einer Seite wegkippt und der ausbalancierenden Bewegung so lang wie möglich sein, heißt die Fallzeit sollte so hoch wie möchlich sein, da mit steigender Stablänge sich die Fallzeit erhöht. Es folgt also es ist umso leichter einen Stab zu balancieren je länger er ist.
Numerische Lösung/ Computerprogramm
Vorgehen Zeitschrittverfahren
Das Zeitschritt- bzw. Euler-Verfahren ist das älteste und einfachste Verfahren um eine Differentialgleichung numerisch zu lösen. Allgemein hat man eine Differentialgleichung welche die Steigung bzw. Beschleunigung eines Punktes beschreibt gegeben. Hat man einen Anfangswert gegeben, so kann man nun auch einen zweiten Wert ermitteln und daraus einen weiteren ermitteln. In unserem Beispiel ist also $\ddot{\varphi}$ abhängig von $\varphi$. $\varphi_0$ und $\dot{\varphi}_0$ sind zum Zeitpunkt 0 bekannt, womit auch $\ddot{\varphi}(0)$ bekannt ist. Wenn wir jetzt den Ort der Stabspitze nach einem Zeitschritt $\Delta t$ nach dem Zeitpunkt $t=0$ wissen wollen, so können wir diesen über die Anfangswerte bestimmen. Es wird angenähert, dass sich im Zeitraum $\Delta t$ die Beschleunigung $\ddot{\varphi}$ sich wie zum Startzeitpunkt verhält. Der Zeitschritt wird mit der vorherigen Beschleunigung multipliziert, um so die neue Geschwindigkeit und somit den neuen Ort zu bestimmen. Beschrieben wird das durch die Formeln: \begin{align} \dot{\varphi}(0+\Delta t)&=\varphi(0)+\Delta t \ddot{\varphi}(0)\\ \varphi(0+\Delta t)&=\varphi(0)+\Delta t \dot{\varphi}(0+\Delta t)\\ \varphi(0+\Delta t)&=\varphi(0)+\Delta t \varphi(0)+\Delta t \ddot{\varphi}(0) \end{align} Zu sehen ist, dass der neue Ort durch bekannte Werte berechnet werden kann. Dadurch kann auch wieder die Beschleunigung der Stabspitze am neuen Ort $\ddot{\varphi}(0+\Delta t)$ berechnet werden. In einer weiteren Iteration kann nun der nächste Punkt berechnet werden.
Endwinkel
Das Programm könnte theoretisch die Winkel für immer größer werdende Winkel simulieren. Da unser Fall aber auf den kippenden Besenstiel beschränkt ist, muss ein Endwinkel eingesetzt werden. Unter der Annahme, dass der Versuch auf komplett ebenen Boden durchgeführt wurde, beträgt dieser natürlich $90^\circ$ also etwa $1.5708$ Radiant.
Länge der Zeitschritte
Eine Veränderung der Schrittlänge hat direkte Auswirkungen auf den letzten Ausgegebenen Wert und die damit verbundene Genauigkeit der Kippzeit. Da die Whileschleife ab einem Winkel von $\varphi=1,5708$ Radiant stoppt, haben größere Schrittweiten zur Folge, dass der letzte berechnete Winkel weiter vom Endwinkel entfernt ist. Damit ist die Kippzeit für größere Schrittweiten etwas kleiner. Die Kippzeit kann dann auch nur eins der Vielfachen der großen Zeitschritte sein. Wählt man jedoch kleinere Zeitschritte so erhält man relativ schnell genauere Kippzeiten.
Der Code
Der unten aufgeführte Code berechnet die Kippzeiten für eine Besenstiellänge von $1,45\,m$. Für die numerischen Werte wurden natürlich die Anfangswerte verändert.
Der Code beginnt mit der Definition der Anfangswerte und der Differentialgleichung. Der Befehl euler ist dann das Herzstück. In einer Module-Umgebung, welche die Anfangswerte als lokal definiert wird eine While-Schleife bis zum Grenzwinkel genutzt, um das Zeitschrittverfahren durchzuführen. Dies wird in eine Liste übertragen. Aus unbekannten Gründen geht dabei die While-Schleife einen Schritt über den Grenzwinkel, weshalb mit Drop der letzte Listeneintrag gelöscht wird. Der nun letzte Eintrag zeigt die Zeit und den zugehörigen Winkel an, also die Kippzeit (stimmt mit der aus Abbildung 3 etwa überein) mit etwa $90^\circ$, je nach Schrittweite. Plottet man jetzt die gesamte Liste erhält man ein Diagramm, welches die Bewegung des Stabes beschreibt.
Um jetzt aber das Diagramm aus Abbildung 3 zu erhalten, muss ein Schritt weiter gegangen werden. In einer weiteren Liste werden nun die letzten Zeitpunkte in Abhängigkeit vom Startwinkel definiert. Dazu wird der Startwinkel in einer äußeren While-Schleife schrittweise erhöht. Der Plot den wir erhalten stimmt ziemlich genau mit Abbildung 3 überein.
- Besenstiel.nb
- t0 = 0;
- \[CurlyPhi]0 = 0.25;
- g = 9.81;
- l = 1.45;
- \[CurlyPhi]10 = 0;
- stepsize = 0.01;
- ans = {{t0, \[CurlyPhi]0}};
- \[CurlyPhi] = \[CurlyPhi]0;
- t = t0;
- \[CurlyPhi]1 = \[CurlyPhi]10;
- \[CurlyPhi]1 = \[CurlyPhi]1 + stepsize*\[CurlyPhi]2[\[CurlyPhi]];
- \[CurlyPhi] = \[CurlyPhi] + stepsize*\[CurlyPhi]1;
- t = t + stepsize;
- ans]
- h = 0.0001;
- \[CurlyPhi]0 = 0.22;
- bns,
- {ans, t, \[CurlyPhi], \[CurlyPhi]1},
- ans = {t0};
- \[CurlyPhi] = \[CurlyPhi]0;
- t = t0;
- \[CurlyPhi]1 = \[CurlyPhi]10;
- \[CurlyPhi] < 1.5708,
- \[CurlyPhi]1 = \[CurlyPhi]1 + h*\[CurlyPhi]2[\[CurlyPhi]];
- \[CurlyPhi] = \[CurlyPhi] + h*\[CurlyPhi]1;
- t = t + h;
- ];
- \[CurlyPhi]0 = \[CurlyPhi]0 + 0.02]; bns];
- acceleration = 1.45*\[CurlyPhi]2[1.5708]
Zeigen Sie, dass ein Massepunkt der Stabspitze mit einer größeren Beschleunigung zu Boden fällt, als eine frei fallende Punktmasse
Die Beschleunigung der Punktmasse am Stabende lässt sich über den Krümmungsradius der Kreisbewegung, also die Stablänge und die Winkelbeschleunigung $\ddot{\varphi}$ beim Aufschlag berechnen. In diesem Moment ist sie nämlich senkrecht nach unten was einen Vergleich ermöglicht. Wie im Code oben zu sehen wurde dazu die Winkelbeschleunigung von $90^\circ$ mit der Stablänge multipliziert woraus sich eine Beschleunigung von $14,715\frac{m}{s^2}$ für die Stabspitze mit voller Masse ergibt. Diese ist deutlich höher als die Beschleunigung einer frei fallenden Punktmasse von $g=9,81\frac{m}{s^2}$.
Versuchsdurchführung
Kippender Besenstiel
Zu Beginn wird eine flache Fläche gesucht an welcher ein Zollstock zur Höhenmessung angeklebt wird. Zur Messung wird noch ein zweiter Zollstock benötigt welcher für die Messung des Abstandes zwischen Wand und Besenstiel verwendet wird. Nun fehlen noch die Art der Zeitmessung und die beiden Besenstiele, wobei die beiden Stiele folgende Werte haben, h1=(159,6±0,3)cm und h2=(133,0±0,3)cm. Für die Zeitmessung wird die akustische Stopuhr der App Phyphox verwendet, als erstes Signal wird ein Stift verwendet und als Endsignal das Auftreffen des Besens auf dem Boden. Um nun einen Winkel festzulegen wird der x-Achsenabschnitt und so der Winkel indirekt festgelegt. Für dieses Vorgehen ist ein rechter Winkel nötig. Der Abstand von Wand zum Besenstiel wird vom Anfang der Wand bis zum Mittelpunkt des Stabquerschnittes gemessen.
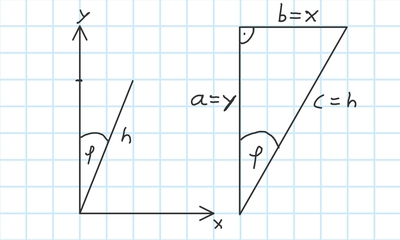

Damit nicht immer eine Wasserwaage oder ähnliches benutzt werden muss, wird der y-Achsenabsschnitt mittels Satz des Pythagoras berechnet. So kann beim Zollstock für die x-Koordinate ein Wert für einen Winkel abgelesen werden und dieser Zollstock muss für einen rechten Winkel lediglich auf einer bestimmten Höhe des y-Zollstockes anliegen, siehe Bild. Die Berechnung folgt über trigonometrische Beziehungen und den Satz des Pytagoras. \begin{align} a^2=c^2-b^2\\ \varphi=arccos(\frac{x}{h}) \end{align}
Messreihe zur Fallzeit des ersten Besenstieles mit h1=(159,6±0,3)cm für verschiedene Winkel $\varphi$ und jeweils fünf Messungen pro Winkel.
| Messung Besen 1 | Winkel in rad | 1 in s | 2 in s | 3 in s | 4 in s | 5 in s | Mittelwert in s | Standardfehler in s |
|---|---|---|---|---|---|---|---|---|
| Winkel 1 | 0,0469±0,0028 | 1,39 | 1,54 | 1,54 | 1,36 | 1,49 | 1,46 | 0,04 |
| Winkel 2 | 0,094 ±0,005 | 1,17 | 1,25 | 1,15 | 1,17 | 1,17 | 1,18 | 0,04 |
| Winkel 3 | 0,126 ±0,006 | 1,02 | 1,01 | 1,01 | 1,00 | 1,01 | 1,01 | 0,04 |
| Winkel 4 | 0,189 ±0,008 | 0,94 | 0,99 | 0,94 | 0,93 | 0,94 | 0,95 | 0,04 |
| Winkel 5 | 0,253 ±0,011 | 0,88 | 0,85 | 0,85 | 0,84 | 0,85 | 0,85 | 0,04 |
Messreihe zur Fallzeit des zweiten Besenstieles mit h2=(133,0±0,3)cm für verschiedene Winkel $\varphi$ und jeweils fünf Messungen pro Winkel.
| Messung Besen 2 | Winkel in rad | 1 in s | 2 in s | 3 in s | 4 in s | 5 in s | Mittelwert in s | Standardfehler in s |
|---|---|---|---|---|---|---|---|---|
| Winkel 1 | 0,0469±0,0028 | 1,25 | 1,33 | 1,34 | 1,32 | 1,32 | 1,31 | 0,04 |
| Winkel 2 | 0,094 ±0,005 | 1,08 | 1,11 | 1,09 | 1,11 | 1,10 | 1,10 | 0,04 |
| Winkel 3 | 0,126 ±0,006 | 0,98 | 1,01 | 0,99 | 0,99 | 0,97 | 0,99 | 0,04 |
| Winkel 4 | 0,189 ±0,008 | 0,87 | 0,87 | 0,87 | 0,85 | 0,85 | 0,86 | 0,04 |
| Winkel 5 | 0,253 ±0,011 | 0,79 | 0,75 | 0,77 | 0,75 | 0,74 | 0,76 | 0,04 |
Luftreibung
 Der Grundaufbau bleibt gleich. Es werden nun Messungen für zwei verschiedene Winkel durchgeführt, einmal werden die beiden Winkel gemessen mit einem kleinen Pappestück welches an dem Besenstiel befestigt wird, siehe Bild, und dann werden diese Messungen mit einem größeren Pappestück wiederholt. Als Winkel werden der Einfachheit halber und der besseren Möglichkeit eines späteren Vergleiches Winkel 1 und Winkel 5 aus der vorherigen Messung verwendet. Als Besenstiel wird Besen 1 aus ebenfalls der obigen Messung verwendet mit h1=(159,6±0,3)cm. Die Pappoberflächen wurden gemessen mit APappe-1=(0,300±0,003)m2 und APappe-2=(0,532±0,004)m2.
Der Grundaufbau bleibt gleich. Es werden nun Messungen für zwei verschiedene Winkel durchgeführt, einmal werden die beiden Winkel gemessen mit einem kleinen Pappestück welches an dem Besenstiel befestigt wird, siehe Bild, und dann werden diese Messungen mit einem größeren Pappestück wiederholt. Als Winkel werden der Einfachheit halber und der besseren Möglichkeit eines späteren Vergleiches Winkel 1 und Winkel 5 aus der vorherigen Messung verwendet. Als Besenstiel wird Besen 1 aus ebenfalls der obigen Messung verwendet mit h1=(159,6±0,3)cm. Die Pappoberflächen wurden gemessen mit APappe-1=(0,300±0,003)m2 und APappe-2=(0,532±0,004)m2.
Messreihe zur Fallzeit des ersten Besenstieles mit h1=(159,6±0,3)cm unter Einfluss größerer Reibung durch ein Pappestück für zwei verschiedene Winkel $\varphi$, zwei verschiedene Pappestücke und jeweils fünf Messungen pro Winkel und Pappe.
| Reibung Besen 1 | Winkel in rad | 1 in s | 2 in s | 3 in s | 4 in s | 5 in s | Pappoberfläche in m2 | Mittelwert in s | Standardfehler in s |
|---|---|---|---|---|---|---|---|---|---|
| Winkel 1 | 0,0469±0,0028 | 1,65 | 1,65 | 1,60 | 1,55 | 1,58 | 0,300±0,003 | 1,60 | 0,04 |
| Winkel 1 | 0,0469±0,0028 | 1,92 | 1,90 | 1,91 | 1,89 | 1,92 | 0,532±0,004 | 1,91 | 0,04 |
| Winkel 5 | 0,253 ±0,011 | 0,97 | 0,94 | 0,99 | 0,97 | 0,97 | 0,300±0,003 | 0,97 | 0,04 |
| Winkel 5 | 0,253 ±0,011 | 1,08 | 1,13 | 1,11 | 1,12 | 1,12 | 0,532±0,004 | 1,11 | 0,04 |
Numerische Werte
Durch das Computerprogramm bestimmte numerische Werte. Dienen dem Vergleich zu den experimentellen Werten. h1 ist der erste und h2 der zweite Besenstiel.
| Numerisch Besen 1,2 | Winkel in rad | Werte für h1 | Werte für h2 |
|---|---|---|---|
| Winkel 1 | 0,0469 | 1,398 | 1,279 |
| Winkel 2 | 0,0941 | 1,170 | 1,070 |
| Winkel 3 | 0,1257 | 1,075 | 0,983 |
| Winkel 4 | 0,1890 | 0,941 | 0,861 |
| Winkel 5 | 0,2533 | 0,846 | 0,773 |
