meta data for this page
Besenstiel -- gruppe316
Der Versuch wurde durchgeführt von: Aylin Talu und Anna Paul
Die Wiki-Seite wurde angelegt am: 5 January 2021 14:48
Diese Wiki-Seite behandelt den Home-Lab Versuch “Kippender Besenstiel”. Hierbei wird die Fallzeit t eines Besenstiels der Länge l in Abhängigkeit vom Startwinkel phi bestimmt und mit numerisch bestimmten Werten verglichen.
Versuchsdurchführung
Messung 1
 Die erste Messung (Ay) mit einem Besen der Länge l=1,2m wurde draußen vor einer weißen Wand durchgeführt. An diese Wand wurde ein Zollstock geklebt, damit die Anfangswinkel besser bestimmt werden können. Da die Messung für jeden Winkel fünf mal durchzuführen ist, wurden die Startwinkel an der Wand mit Kreide markiert, wie es in Abb.1 zu erkennen ist.
Die erste Messung (Ay) mit einem Besen der Länge l=1,2m wurde draußen vor einer weißen Wand durchgeführt. An diese Wand wurde ein Zollstock geklebt, damit die Anfangswinkel besser bestimmt werden können. Da die Messung für jeden Winkel fünf mal durchzuführen ist, wurden die Startwinkel an der Wand mit Kreide markiert, wie es in Abb.1 zu erkennen ist.
Die Bodenbeschaffenheit und das mit einer Art Gummi verkleidete Ende des Besenstiels haben bereits dazu beigetragen, dass der Stab beim Fallen nicht verrutscht. Der Besen wurde anhand einer Markierung am Boden möglichst immer an der gleichen Stelle zwischen zwei Steinplatten positioniert, anhand der Linien an der Wand in den richtigen Winkel versetzt und schließlich einfach losgelassen.
Dieser Link enthält das Video, in dem der Versuch für die ersten 4 Winkel durchgeführt worden ist.
Messung 2
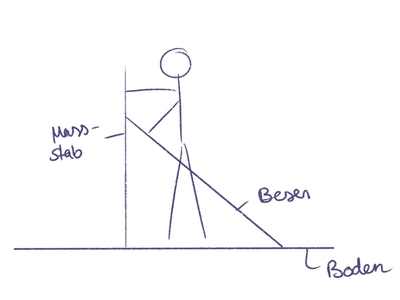
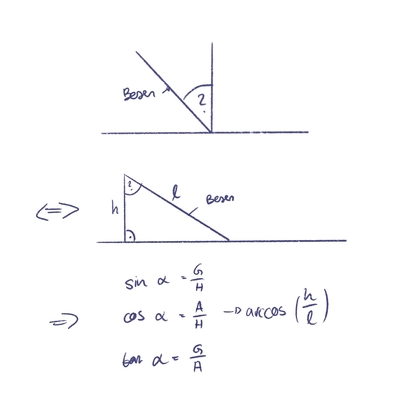
Bei der zweiten Messung (An) wurde ein Handtuch auf dem Boden ausgebreitet, um diesen zu schützen. Der Besen wurde jeweils fünf mal von dem gleichen Winkel aus fallen gelassen. Um dies zu erreichen, wurde ein Massstab genutzt um die Höhe des Besens gleich zu lassen. Der Winkel wurde im Anschluss wie in Grafik … zu sehen ist bestimmt.
Messung 3 Luftwiderstand
Die Messung 3 wurde Identisch zur Messung 2 durchgeführt, jedoch wurde um den Einfluss des Luftwiderstandes zu Untersuchen, an den Besen ein Starkes Blatt Papier geklebt (130g/m^2) (siehe Foto). Der Besen wurde dann auch 5 mal bei gleichbleibenden Winkel fallen gelassen und mit dem gleichen Winkel ohne das Papier verglichen.
Zeitmessung
Um den Fehler bei der Zeitmessung zu minimieren, wurde das Experiment per Video aufgezeichnet. Somit muss keine Schrecksekunde berücksichtigt werden und es kann eine genaue Angabe über die Fallzeit gemacht werden. Die Videos wurden in einem Schnittprogramm hochgeladen
Zur Zeitmessung wurde ein Video aufgenommen, welches im Nachhinein analysiert wurde. Hierbei wurde Video An in 25 fps und Video Ay in 30 fps geschossen. Bei den Videos wurden die genauen Frames bestimmt, bei denen der Besen losgelassen wurde und bei welchem er auf dem Boden aufschlug. Durch die Differenz wurde die Zeit bestimmt, die der Besen zum Fallen brauchte.
Für die Unsicherheit wurden jeweils 3fps angenommen. Ein Frame zu Anfang beim Loslassen, eins beim Aufschlagen und eins fürs menschliches Versagen. Dies wirkt sich bei den Unterschiedlichen Videos natürlich anders auf die Sekunden aus. Bei Video An entspricht dies +- 0,12 sec und bei dem Video Ay +- 0,1 sec.
Im Anschluss folgt ein screenshot um besser sehen zu können wie genau die Zeit gemessen wurde.
Ein Ausschnitt der Excel Tabelle von Messung 1 Ay. Hierbei ist zu bemerken, dass bei der Zeit (aa:bb:cc:dd) aa für die Stunden, bb für die Minuten, cc für die Sekunden und dd für die fps steht.
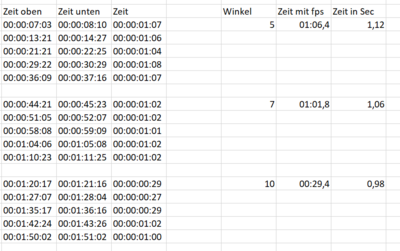
Messdaten
In der ersten Tabelle befinden sich die Messwerte zur ersten Messung mit einem Besen der Länge l=1,2m. Für die Fallzeiten wurde bereits der Mittelwert aller 5 Messungen bestimmt, der auch später in der Auswertung verwendet wird. Die zweite Tabelle enthält die Daten zur Messung mit einem Besen der Länge l=1,34m.
| Winkel in Grad | Mittelwert der Fallzeit in Sekunden | Simulierte Fallzeit |
|---|---|---|
| 5 | 1,21 | 1,03 |
| 7 | 1,06 | 0,95 |
| 10 | 0,98 | 0,85 |
| 12 | 0,88 | 0,79 |
| 17 | 0,75 | 0,69 |
| 23 | 0,66 | 0,6 |
| 27 | 0,63 | 0,56 |
| 32 | 0,55 | 0,51 |
| 37 | 0,50 | 0,46 |
| 42 | 0,47 | 0,43 |
| 50 | 0,40 | 0,37 |
| 54 | 0,38 | 0,35 |
| 59 | 0,35 | 0,31 |
| Winkel in Grad | Mittelwert der Fallzeit in Sekunden | Simulierte Fallzeit |
|---|---|---|
| 9,9 | 1,08 | 0,9 |
| 17,2 | 0,84 | 0,73 |
| 22,3 | 0,76 | 0,65 |
| 25,4 | 0,73 | 0,61 |
| 33,3 | 0,59 | 0,53 |
| 35,6 | 0,56 | 0,5 |
| 42,4 | 0,57 | 0,45 |
| 46,6 | 0,49 | 0,42 |
| 48,4 | 0,48 | 0,41 |
Computerprogramm
Zeitschrittverfahren
Das Computerprogramm zum numerischen Lösen der Differentialgleichung mit dem Zeitschrittverfahren wurde in einem Mathematica Notebook geschrieben. Hierbei wurden die Besenlänge l=1.45m und der Anfangswinkel phi0= 0.25 rad gewählt. Zunächst wird in “bewegung” das Zeitschrittverfahren angewandt, um den Winkel in Abhängigkeit von der Zeit zu erhalten und somit den Bewegungsverlauf der Besenspitze. Der erste Wert dieser Liste gibt uns somit den Startwinkel und der letzte Wert die Fallzeit. Dies wird eingebunden in “weitere”, um das erste Tupel aus Anfangswinkel und Fallzeit zu erhalten. Weiterhin wird eine Liste erstellt, die die Fallzeit für größer werdende Winkel angibt und schließlich kann das ganze mit dem in Mathematica eingebauten Befehl ListPlot gezeichnet werden. Zum genaueren Untersuchen der Werte ist es jedoch von Vorteil, sich die Listen ausgeben zu lassen.
l = 1.45;
\[CurlyPhi]0 = 0.25;
g = 9.81;
zeitschritt = 0.005;
\[Tau] = Sqrt[(2 l)/(3 g)];
bgl[\[CurlyPhi]_] := Sin[\[CurlyPhi]]/\[Tau]^2;
bewegung := Module[{liste, t, \[CurlyPhi], \[CurlyPhi]1},
t = t0; t0 = 0; \[CurlyPhi] = \[CurlyPhi]0;
t = t0; \[CurlyPhi]1 = 0;
liste = {{\[CurlyPhi]0, t0}};
While[\[CurlyPhi] < \[Pi]/
2, \[CurlyPhi]1 = \[CurlyPhi]1 + zeitschritt*bgl[\[CurlyPhi]];
\[CurlyPhi] = \[CurlyPhi] + zeitschritt*\[CurlyPhi]1;
t = t + zeitschritt;
liste = Append[liste, {\[CurlyPhi], t}]]; liste];
weitere =
Module[{\[CurlyPhi]0, lüst},
lüst = {{First[First[bewegung]], Last[Last[bewegung]]}};
\[CurlyPhi]0 = 0.25;
While[\[CurlyPhi]0 < \[Pi]/2,
lüst = Append[
lüst,
{\[CurlyPhi]0, Last[Module[
{liste, t, \[CurlyPhi], \[CurlyPhi]1},
liste = {t0};
\[CurlyPhi] = \[CurlyPhi]0;
t = t0;
\[CurlyPhi]1 = 0;
While[
\[CurlyPhi] < \[Pi]/2,
\[CurlyPhi]1 = \[CurlyPhi]1 + zeitschritt*bgl[\[CurlyPhi]];
\[CurlyPhi] = \[CurlyPhi] + zeitschritt*\[CurlyPhi]1;
t = t + zeitschritt;
liste = Append[liste, t] ];
liste]]}]; \[CurlyPhi]0 = \[CurlyPhi]0 + 0.01]; lüst];
ListPlot[weitere,
AxesLabel -> {"Anfangswinkel \!\(\*SubscriptBox[\(\[CurlyPhi]\), \(0\
\)]\) in rad", "Fallzeit t in s"}, ImageSize -> Large,
GridLines -> {{.2, .4, .6, .8, 1.0, 1.2, 1.4,
1.6}, {.1, .2, .3, .4, .5, .6, .7, .8}}, PlotLabel -> "Fallzeit"]
Die entstehende Grafik sieht dann wie folgt aus:
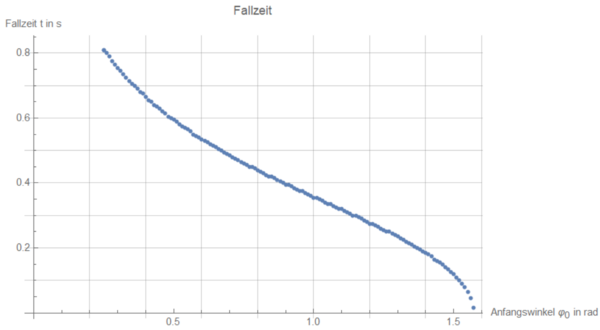
Um schließlich Aussagen treffen zu können über den Einfluss der Zeitschritte auf die simulierte Fallzeit, kann man sich entweder die gesamte Liste Ausgeben lassen, z.B bei einem Zeitschritt von 0.03s:
In: bewegung
Out: {{0.25, 0}, {0.25226, 0.03}, {0.256799, 0.06}, {0.263658,
0.09}, {0.272897, 0.12}, {0.284598, 0.15}, {0.298864,
0.18}, {0.315819, 0.21}, {0.33561, 0.24}, {0.358409,
0.27}, {0.384413, 0.3}, {0.413841, 0.33}, {0.446943,
0.36}, {0.483992, 0.39}, {0.525291, 0.42}, {0.57117,
0.45}, {0.621986, 0.48}, {0.678125, 0.51}, {0.739993,
0.54}, {0.808019, 0.57}, {0.882649, 0.6}, {0.964333,
0.63}, {1.05352, 0.66}, {1.15065, 0.69}, {1.25612, 0.72}, {1.37027,
0.75}, {1.49337, 0.78}, {1.62558, 0.81}}
Da man an dieser Stelle aber die Fallzeit erhalten möchte, reicht es sich den letzten Wert anzusehen:
In: Last[bewegung]
Out: {1.62558, 0.81}
Hierbei fällt jedoch auf, dass für größere Zeitschritte der letzte Wert meist einen Anfangswinkel enthält, der größer als 90° ist. Für Winkel größer als 90° sollte das Zeitschrittverfahren jedoch bereits enden. Je kleiner also die Zeitschritte sind, desto präziser wird die Fallzeit bestimmt.
Einfluss Besenlänge und Anfangswinkel
Eine weitere Visualisierung der Bewegungs außerhalb des Zeitschrittverfahrens ist mit folgendem separaten Code ersichtlich:
g := 9.81;
\[Tau][l_] := Sqrt[(2 l)/(3 g)];
sol[\[CurlyPhi]0_, l_] :=
NDSolve[{\[CurlyPhi]''[t] ==
Sin[\[CurlyPhi][t]]/\[Tau][l]^2, \[CurlyPhi][
0] == \[CurlyPhi]0, \[CurlyPhi]'[0] == 0}, {\[CurlyPhi][
t], \[CurlyPhi]'[t], \[CurlyPhi]''[t], \[CurlyPhi]'''[t] }, {t, 0,
2}]
Plot[Evaluate[{\[CurlyPhi][t], \[CurlyPhi]'[t], \[CurlyPhi]''[
t], \[CurlyPhi]'''[t]} /. sol[0.25, 1.45]], {t, 0, 1},
AxesLabel -> {"x", "y"}, GridLines -> Automatic,
PlotLabel ->
"Numerische Lösung der Bewegungsgleichung und ihre Ableitungen",
PlotLegends -> Automatic, ImageSize -> Large]
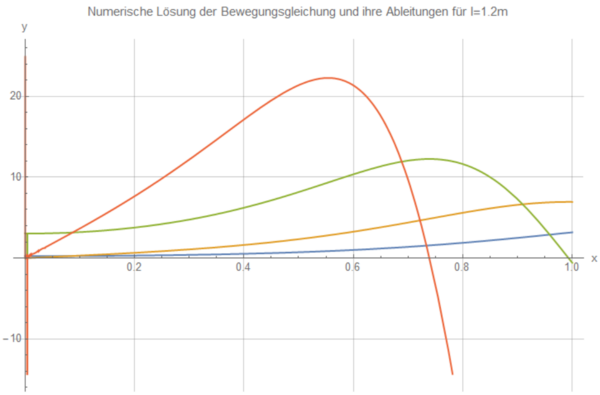
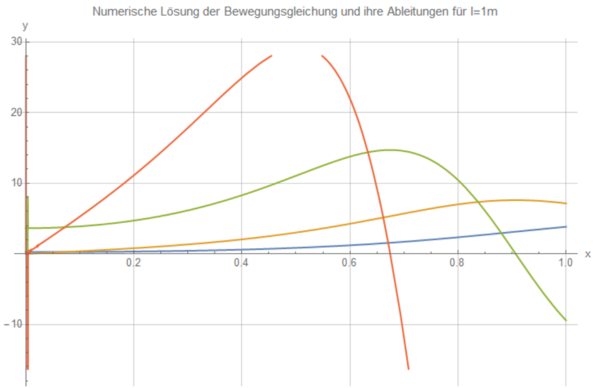
Der sich ergebende Plot ist gut geeignet, um qualitative Aussagen über die Fallzeit zu treffen, denn die Nullstelle der dritten Ableitung gibt diese an. Dies hängt natürlich damit zusammen, dass die Beschleunigung beim Aufprall auf den Boden am größten ist und die Funktion der Beschleunigung, also die zweite Ableitung, dort ihr Maximum hat. Daran lässt sich der Einfluss der Stablänge zeigen.
Der folgende Plot gehört zum obigen Code mit der Besenlänge l=1.45m:
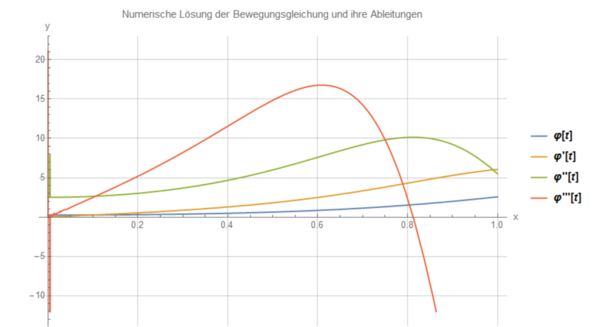
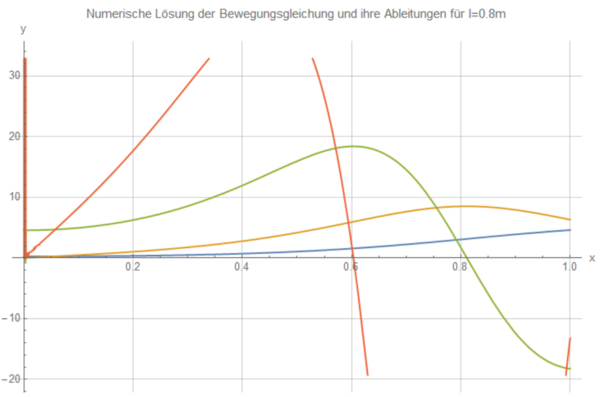
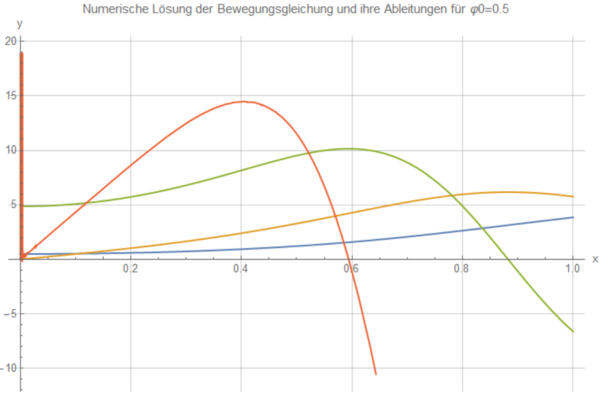
Die Legende gilt auch für die weiteren Plots. Die nachfolgenden beschreiben die Bewegung eines Besens der Länge l=1.2m, 1.0m, 0.8m:
Man erkennt, dass die Nullstelle des orangenen Graphen immer weiter nach links wandert, je kürzer der Besen ist. Je länger also ein Besenstiel ist, desto länger ist auch die Fallzeit. Mit dem gleichen Verfahren lässt sich auch zeigen, dass die Fallzeit für kleinere Winkel größer ist.
In einer reibungsfreien Umgebung hat die Masse keinen Einfluss auf die Fallzeit, sie wird aus der Bewegungsgleichung rausgekürzt.
Beschleunigung der Stabspitze
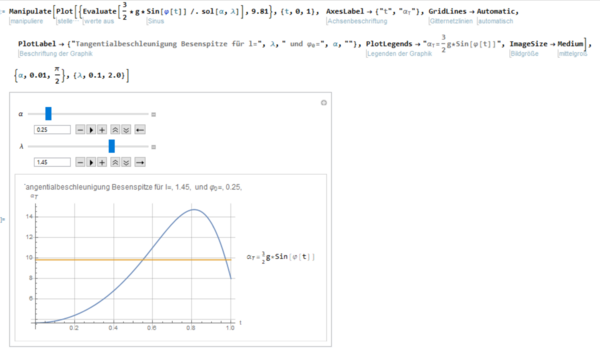
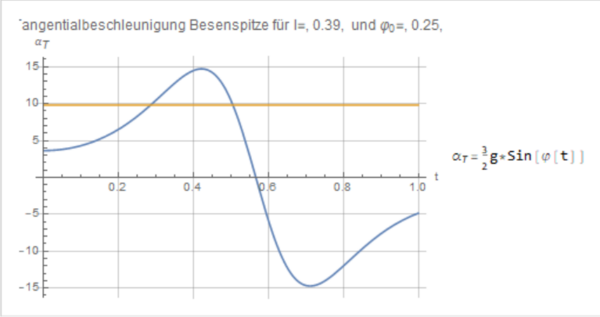
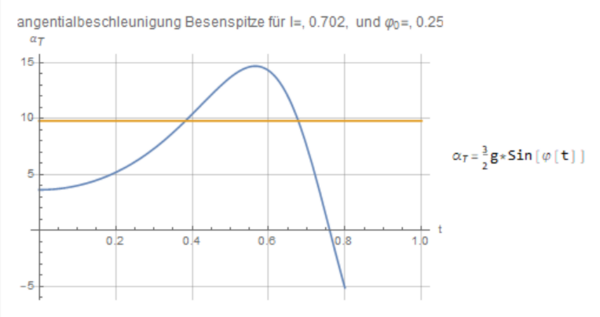
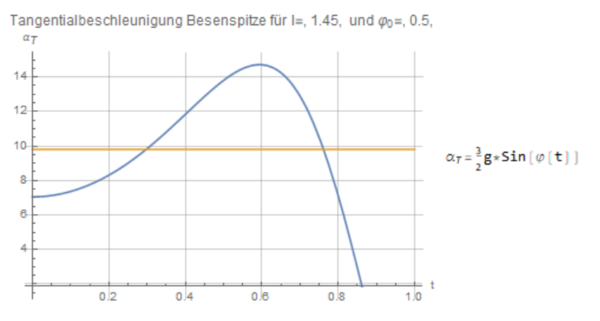
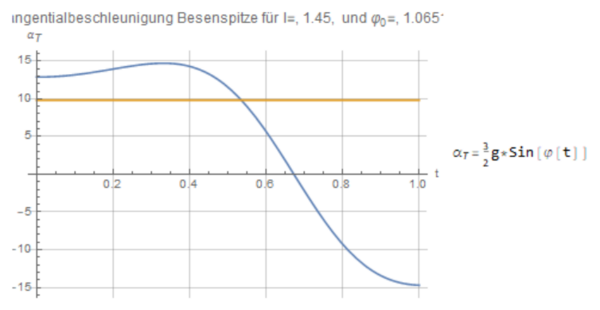
Es wird weiterhin im selben Notebook gearbeitet wie im vorherigen Abschnitt. Hier soll gezeigt werden, dass die Beschleunigung der Stabspitze eines beliebig langen Besens zu einem beliebigen Anfangswinkel mit einer größeren Beschleunigung zu Boden fällt als eine frei fallende Punktmasse. Die Herleitung der Formel erfolgt in unserem Versuchsbericht im Unterkapitel “Beschleunigung”. Mit dem folgenden Code wurde eine Manipulate Umgebung erstellt, in der die Besenlänge und der Anfangswinkel variiert werden können. Der Plot stellt die Tangentialbeschleunigung dar. Für unsere Betrachtung ist nur das erste Maximum von Bedeutung, alle weiteren, die eventuell auftreten, können vernachlässigt werden. Außerdem wurde eine Linie eingezeichnet, die den Wert der Fallbeschleunigung markiert.
Manipulate[
Plot[{Evaluate[
3/2*g*Sin[\[CurlyPhi][t]] /. sol[\[Alpha], \[Lambda]]], 9.81}, {t,
0, 1.5},
AxesLabel -> {"t", "\!\(\*SubscriptBox[\(\[Alpha]\), \(T\)]\)"},
GridLines -> Automatic,
PlotLabel -> {"Tangentialbeschleunigung Besenspitze für l=", \
\[Lambda],
" und \!\(\*SubscriptBox[\(\[CurlyPhi]\), \(0\)]\)=", \[Alpha],
""}, PlotLegends ->
"\!\(\*SubscriptBox[\(\[Alpha]\), \
\(T\)]\)=\!\(\*FractionBox[\(3\), \(2\)]\)g*Sin[\[CurlyPhi][t]]"], {\
\[Alpha], 0.01, \[Pi]/2}, {\[Lambda], 0.1, 2.0}]
Nun wird für einige beliebige Werte exemplarisch gezeigt, dass die Stabspitze mit einer höheren Beschleunigung fällt als eine Punktmasse es tun würde.