Besenstiel -- Gruppe306

Der Versuch wurde durchgeführt von: Henrik Martens und Jonas Musall
Die Wiki-Seite wurde angelegt am: 18 December 2020 11:39

Auch wenn in Mathematica bereits der Befehl NDSolve existiert, der eine DGL numerisch löst, kann selbstverständlich auch ein eigenes Verfahren implementiert werden. Die dafür zuständige Methode ist “solDiff”, welche als Input die Länge l, die Anfangswerte φ₀ und φ'₀, den Zeitraum, sowie die Intervallgröße verlangt. Dann wird in einer Umgebung mit lokalen Variablen zunächst eine Tabelle erstellt, welche zunächst nur Nullen enthält und der folgenden Form ist:

{{0,0,0,0},{0,0,0,0},...,{0,0,0,0}}  

In diese Tabelle werden dann Zeiten, Winkel, Winkelgeschwindigkeit und Winkelbeschleunigung eingetragen, die zusammen eine numerische Lösung ergeben. Dazu wird in einer For-Schleife die Zeit schrittweise erhöht und für jeden Zeitpunkt der neue Winkel berechnet. Ist dieser irgendwann größer als π/2, wird der Winkel für die restliche Zeit auf π/2 (sowie Geschwindigkeit und Beschleunigung auf 0) gesetzt und die Fallzeit in einer Variablen abgespeichert. Die Funktion gibt dann die Tabelle mit den Punkten sowie die Fallzeit für diese Bewegung zurück.

Um φ(t) und deren Ableitungen zu bekommen, können die Methoden “solphi”, “soldphi” und “solddphi” verwendet werden, welche aus der ausgegebenen Tabelle von “solDiff” die richtigen Werte extrahieren.

Praktikum_Besenstiel.nb

solDiff[l_, phi0_, dphi0_, tmax_, dt_] := Module[{phi = phi0, dphi = dphi0, ddphi = 0, finalList, list = ConstantArray[0, Floor[tmax/dt] + 1], t0, tFall = -1},
  finalList = Transpose[{list, list, list, list}];
 
  For[t0 = 0, t0 <= tmax, t0 += dt,
 
   finalList[[t0/dt + 1, 4]] = ddphi;
   finalList[[t0/dt + 1, 3]] = dphi;
   finalList[[t0/dt + 1, 2]] = phi;
   finalList[[t0/dt + 1, 1]] = t0;
 
   If[phi >= Pi/2,
    If[tFall == -1, tFall = t0];
    phi = Pi/2; dphi = 0;ddphi = 0;,
 
    ddphi = Sin[phi]/((2*l)/(3*9.81));
    dphi += dt*ddphi;
    phi += dt*dphi;]
   ];
  {finalList, tFall}
  ]
 
solphi[l_, phi0_, dphi0_, tmax_, dt_] := Transpose[{solDiff[l, phi0, dphi0, tmax, dt][[1, All, 1]], solDiff[l, phi0, dphi0, tmax, dt][[1, All, 2]]}]
 
soldphi[l_, phi0_, dphi0_, tmax_, dt_] := Transpose[{solDiff[l, phi0, dphi0, tmax, dt][[1, All, 1]], solDiff[l, phi0, dphi0, tmax, dt][[1, All, 3]]}]
 
solddphi[l_, phi0_, dphi0_, tmax_, dt_] := Transpose[{solDiff[l, phi0, dphi0, tmax, dt][[1, All, 1]], solDiff[l, phi0, dphi0, tmax, dt][[1, All, 4]]}]

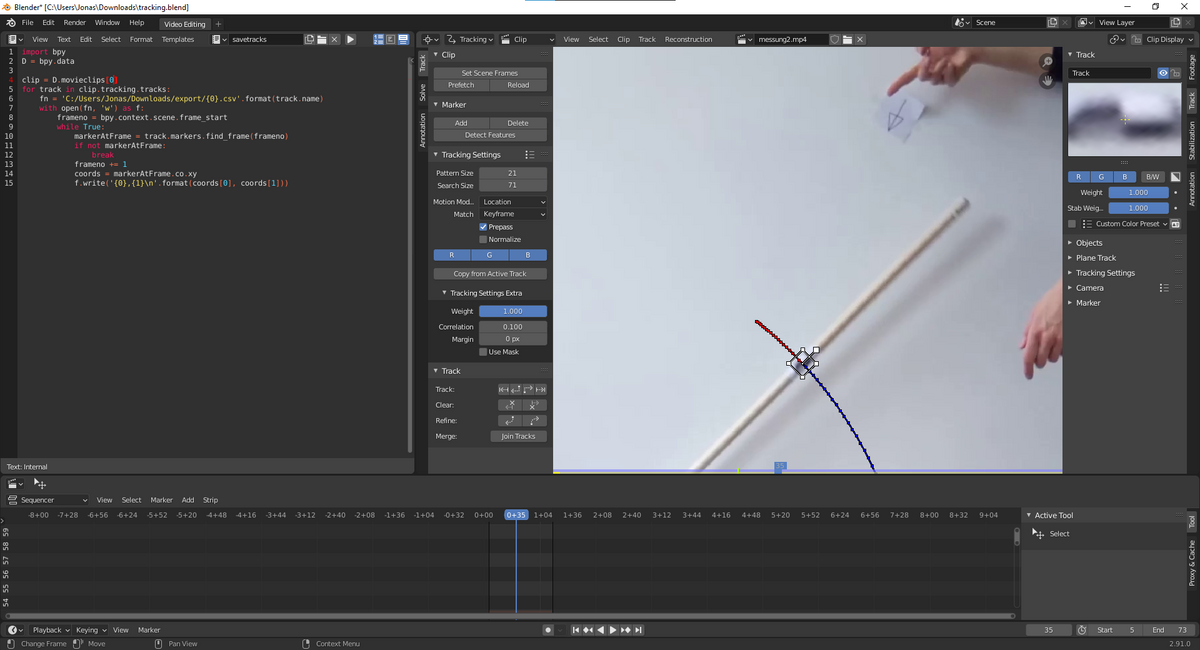
Um die praktisch durchgeführten Versuche auszuwerten, wurde der umfallende Besenstiel auf Video aufgenommen. Der Winkel kann dann durch Tracken eines auf dem Stiel angebrachten Markers in Blender (GPL-lizensierte 3D Suite, die auch zur Videoanalyse genutzt werden kann) und der bekannten Position des Auflagepunktes errechnet werden. Zusätzlich wurde aus dem Videobild errechnet welcher Winkel die Kamera zur Waagerechten hatte.

Im Folgenden Bilder und ein Video des Versuchsaufbaus, sowie ein Screenshot aus dem Analyseprozess in Blender.

Die Positionen der Marker wurden mithilfe eines Python-Skriptes in Tabellen exportiert.

import bpy
D = bpy.data
 
clip = D.movieclips[0]
for track in clip.tracking.tracks:
    fn = 'C:/Users/Jonas/Downloads/export/{0}.csv'.format(track.name)
    with open(fn, 'w') as f:
        frameno = bpy.context.scene.frame_start
        while True:
            markerAtFrame = track.markers.find_frame(frameno)
            if not markerAtFrame:
                break
            frameno += 1
            coords = markerAtFrame.co.xy
            f.write('{0},{1}\n'.format(coords[0], coords[1]))

Langer Stiel, L = (1.3050±0.0005)m

Kurzer Stiel, L = (0.3750 ± 0.0005)m

Erhöhter Luftwiderstand, kurzer Stiel