meta data for this page
Drehschwingung - Gruppe 342
Lukas Köpp 10029243
Julius Riekenberg 10025155
Aufstellen der Bewegungsgleichung
Wir betrachten beim Drehpendel die Kraft, die auf ein Objekt beim Drehen um die Aufhängungsachse wirkt. Diese übersetzt sich mittels des Trägheitswiderstandes in eine Winkelbeschleunigung
$I \ddot{\phi} = D = - D_R \phi $
Dabei bezeichnen wir: $I$ den Trägheitsmoment, $D$ in $[Nm]$ Drehmoment, $D_R$ in $[Nm/rad]$ Winkelrichtgröße und $\phi$ in $[rad]$ Winkelauslenkung der Aufhängung. $[rad] = 1$ gibt hier nur an, dass es sich um einen Winkel im Bogenmaß handelt.
Insbesondere ist die Winkelrichtgröße gegeben als
$D_R = \frac{\pi}{2} \frac{G r^4}{L}$
mit $r$ Radius der Aufhängung, $G$ Torsionsmodul (Materialkonstante) und $L$ Länge des Drahtes.
Wir sehen also an $D_R \propto r^4$, dass eine kleine Erhöhung im Drahtradius das Drehmoment stark beeinflusst. Verdoppeln wir die Dicke erhalten wir also $D_R' = 2^4 D_R = 16 D_R$ also eine Ver-16-fachung des Drehmoments.
Lösung der Bewegungsgleichung
Wir kennen die Basislösung $\phi(t) = A \sin{\omega t} + B \cos{\omega t}$ mit $\dot{\phi}(t) = A \omega \cos{\omega t} - B \omega \sin{\omega t}$ für die DGL. Betrachten wir nun das Auslenken des Pendels um $\phi(0) = \phi_0$ und das Loslassen ohne Anfangsgeschwindigkeit $\dot{\phi}(0) = \dot{\phi}_0$ erhalten wir
$\dot{\phi}(0) = A \omega \cos{0} - B \omega \sin{0} = A \omega = 0 \rightarrow A = 0 $
$\phi_0 = B \cos{0} = \phi_0 \rightarrow B = \phi_0$
Wir erhalten also $\phi(t) = \phi_0 \cos{\omega t}$ als Bahnkurve. Einsetzen in die DGL
$I \ddot{\phi} = D = - D_R \longleftrightarrow I \phi_0 (-\omega^2) \cos{\omega t} = - D_R \phi_0 \cos{\omega t} \longrightarrow \omega^2 = \frac{D_R}{I}$.
Damit können wir die Periodendauer angeben
$ T_{Periode} = \frac{1}{f} = \frac{1}{2 \pi \omega} = \frac{1}{2 \pi} \sqrt{\frac{I}{D_R}}$
Unter der Annahme eines harmonischen Potentials können wir die Periodendauer $T \neq T(\phi_0)$ als konstant ansehen. Somit ist $T_{Schwingungsdauer} = T_{Periode} := T$
$ T := T(L) = \frac{1}{2 \pi} \sqrt{\frac{2 I L}{\pi G r^4}} = \frac{1}{2 \pi r^2} \sqrt{\frac{2 I}{\pi G}} \cdot \sqrt{L}$
Für $T^2$ finden wir einen linearen Zusammenhang:
$ T^2 = \frac{I}{2 \pi^3 G r^4} \cdot L $
Durchführung
Wir hängen also starre Körper verschiedener Geometrien an unterschiedlichen Aufhängungen auf. Nun lenken wir die Körper um einen Anfangswinkel $\phi_0$ aus und lassen sie ohne Anfangsgeschwindigkeit los. Nun messen wir zur Verbesserung der Genauigkeit die Zeit $T_n$ über $n$ Perioden. Durch das mitteln verkleinert sich unsere Messunsicherheit in der Zeit.
Abhängig von der Dämpfung Aufhängung, dem Trägheitsmoment des Körpers und dem Torsionsmodul $G$ wählen wir $\phi_0$ und $n$ sinnvoll. Der Schnürsenkel dämpft hier zum Beispiel stark, hat jedoch eine sehr geringe rücktreibende Kraft sodass wir $n$ klein und $\phi_0$ groß wählen.
Wir fangen damit an, das Torsionsmodul $G$ unter Bekanntheit des Trägheitsmoments $I$ des Stabes zu bestimmen. Dies erlaubt uns, im späteren Teil des Versuches Trägheitsmomente $I$ unbekannter Körper zu bestimmen. Wir errechen auch hier ein theoretisches Trägheitsmoment und vergleichen.
Energiebetrachtung
Wir interessieren uns für eine infinitesimale Winkeländerung $d\phi$. Die Arbeit $W$ entspricht dabei
$ W = \int D d\phi \longrightarrow \frac{dW}{d\phi} = \frac{d}{d\phi}\int D d\phi = D $
Umstellen liefert also
$dW = D \cdot d\phi$
Betrachten wir die Rotationsenenergie $E = \frac{1}{2} I (\frac{d\phi}{dt})^2$
$\frac{dE}{dt} = \frac{dE}{d\phi}\frac{d\phi}{dt} = I \frac{d^2\phi}{dt^2} \frac{d\phi}{dt} \longleftrightarrow dE = I \ddot{\phi} \cdot d\phi $
Gleichsetzen von $E = W$ liefert schließlich mit $D = - D_R \phi$
$ I \ddot{\phi} = D = - D_R \phi $
Wir erhalten unsere DGL also auch mittels einer Energiebetrachtung.
Steiner'scher Satz
Unter Kenntnis des Trägheitsmomentes starrer Körper mit Gesamtmasse $M$ um eine feste Achse durch den Schwerpunkt $I_S$ erlaubt der Steiner'sche Satz die Berechnung des Trägheitsmomentes $I'$ um eine parrelel um $d$ verschobene Achse:
$I' = I_S + M d^2 $
Zur Herleitung benötigen wir nur die Vektoraddition $\vec{x} = \vec{x'} + \vec{\delta x}$ und die Definition des Schwerpunktes als Punkt, an dem die Integrale $\int_V \rho \cdot r_i = 0$ für $r = (x,y,z)$ verschwinden.
Wir betrachten also das Trägheitsmoment I' entlang einer Achse $\vec{n}$ und setzen den Urspung des Koordinatensystem in den Schwerpunkt und die z-Achse parallel zur Drehachse. Damit gilt für den Abstand r eines Punktes zur Drehachse
$ r^2 = (\delta x)^2 + (\delta y)^2$
Setzen wir ein in die Definition des Trägheitsmomentes mit Massendichte $\rho$
$I' = \int_V \rho (\delta x)^2 + (\delta y)^2$
$I' = \int_V \rho (x - x')^2 + (y-y')^2$
Terme aufdröseln:
$I' = \int_V \rho x^2 + y^2 + \int_V \rho x'^2 + y'^2 $
$I' = I_S + (x'^2 + y'^2) \cdot \int_V \rho - 2 y' \int_V \rho x - 2 x' \int_V \rho y$
$I' = I_S + M d^2 $
mit $d = (x'^2 + y'^2)$ ist der Steiner'sche Satz.
Berechnung der Trägheitsmomente mittels der Geometrie
Wir berechnen die Trägheitsmomente $I$ nach der Formel
$ I=\int _{V}{\vec {r}}_{\perp }\!^{2}\rho ({\vec {r}})\mathrm {d} V $
wobei wir die Massendichte $\rho({\vec {r}}) = const. $ annehmen.
Die hohe Unsicherheit ist damit zu erklären, dass wir keine Küchenwaage besitzen. Wir bauen uns also folgende Apparatur auf:
Zuerst messen wir das Gewicht gegen die Füllhöhe der Flasche mit $u(\delta m) = 0,02 kg$. Wir rütteln, um den Einfluss der Haftreibung zu minimieren. Nun messen wir das Nullgewicht $m_0 = 0,07 \pm 0,01 kg$ der Flasche mittels einer Kippwaage. Dazu stellen wir nacheinander leere und volle Shotgläser auf die Waage auf gegenüberliegende Seiten. Mittels der Füllhöhe der Shotgläser und der Dichte von Wasser $\rho \approx 1 kg/m^3$ erhalten wir so also das Gewicht, was wir im folgenden als Summe über $m = \delta m + m_0$ schreiben werden. Die Unsicherheit ist damit $u(m) = 0,03 kg$.
Dünner Metallstab
Aufgrund der Prorportion $r \ll L$ können wir eine Vereinfachung für die Rotation quer durch den Schwerpunkt benutzen. Wir führen eine 1-D Integration entlang des Stabes durch mit 1-D Massendichte $\rho_0 = M/l$:
$I = \rho_0 \int_0^{l/2} r_{\perp }\!^{2} = \rho_0 \frac{1}{3} (\frac{l}{2})^3 = \frac{l}{M} \frac{1}{12} l^3 = \frac{1}{12} M l^2 $
Die exakte Formel auf dem Arbeitsblatt erhalten wir durch 3-D Integration. Für $r \ll L$ fällt der vordere Term aber nicht ins Gewicht.
Für den dünnen Metallstab messen wir
$ l = 0.12 \pm 10^{-3} m, M = 0.04 \pm 0.01 kg $
Nach Gauß'scher Fehlerfortpflanzung gilt:
${u_{I}} = {\sqrt {\left({\frac {\partial I}{\partial M}}\cdot u_{M}\right)^{2}+\left({\frac {\partial I}{\partial l}}\cdot u_{l}\right)^{2}}} $
${u_{I}} = \frac{1}{12} {\sqrt {\left({l^2}\cdot u_{M}\right)^{2}+\left({2Ml}\cdot u_{l}\right)^{2}}}$
${u_{I}} \approx 1,2 \cdot 10^{-5}\ kg\ m^2$
ergibt uns
$I_{Stab} = (4,8 \pm 1,2) \cdot 10^{-5}\ kg\ m^2$
Topfdeckel
Für die Topfdeckel nähern wir die Geometrie als homogonen Zylinder. Wir integrieren also in 2-D Polarkoordinaten mit 2-D Massendichte $\rho_0 = \frac{M}{\pi R^2}$
$ I = \rho_0 \int_0^{2\pi} d\phi \int_0^R r\ dr\ r^2 = \frac{M}{\pi R^2} \ 2\pi\ \frac{1}{4} R^4 = \frac{1}{2}M R^2$
Wir messen die Topfdeckel ab
$R_{1} = d_1/2 = (0.105 \pm 0.0025) m $
$ M_1 = (0.07 + 0.65) \pm 0.03 kg = (0.72 \pm 0.03) kg $
$ R_2 = d_2/2 = (0.085 \pm 0.0025) m$
$M_2 = (0.07 + 0.05) \pm 0.03 kg = (0.12 \pm 0.03) kg$
Die Unsicherheit erhalten wir beinahe analog
${u_{I}} = {\sqrt {\left({\frac {\partial I}{\partial M}}\cdot u_{M}\right)^{2}+\left({\frac {\partial I}{\partial l}}\cdot u_{l}\right)^{2}}} $
${u_{I}} = \frac{1}{2} {\sqrt {\left({R^2}\cdot u_{M}\right)^{2}+\left({2MR}\cdot u_{R}\right)^{2}}}$
${u_{I_1}} \approx 4,18 \cdot 10^{-5}\ kg\ m^2$
${u_{I_2}} \approx 1,86 \cdot 10^{-5}\ kg\ m^2$
Damit ergeben sich die Trägheitsmomente
$ I_1 = (3,97\pm 0,04) \cdot 10^{-3} \ kg\ m^2$
$ I_2 = (0,43\pm 0,02) \cdot 10^{-3} \ kg\ m^2$
Der Fehler ist hier aber eigentlich deutlich größer, da wir von einer homogenen Masseverteilung ausgehen, was offensichtlich nicht der Fall ist.
Messung 1 - Stab an Saite dünn ($r= 0.33 \pm 0.03$)
Anfangsbedingungen:
$\phi_0 = \pi,$ $\dot{\phi}_0 = 0$
Unsicherheiten:
$ u(L) = 0,03m, u(T_{10}) = 0,5s$
| Höhe $L/m$ | Periodendauer $T_{10}/s$ |
|---|---|
| 0,56 | 17,5 |
| 0,42 | 15,9 |
| 0,35 | 15,6 |
| 0,29 | 12,9 |
| 0,24 | 12,58 |
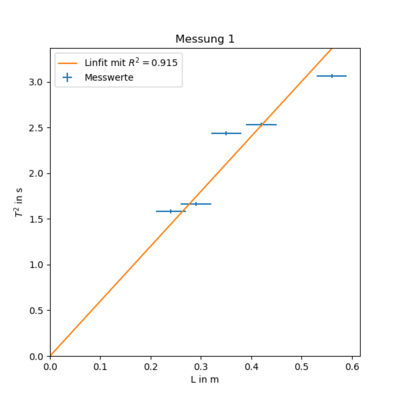
$ T(L)^2 = ( 6.01 \pm 0.27 ) \frac{s^2}{m} \cdot L $
Aus der Theorie erwarten wir eine Steigung die sich aus $st = \frac{I}{2 \pi^3 G r^4}$ zusammensetzt. Außerdem kennen wir schon $ I = (4,8 \pm 1,2) \cdot 10^{-5}\ kg\ m^2 $ und $ r = (0.33 \pm 0.03)mm \Longrightarrow r^4 = ( 12 \pm 5 ) \cdot 10^{-15} m $. Nach Umstellen ergibt sich:
$ G = \frac{I}{2 \pi^3 \cdot st \cdot r^4 } = ( 10 \pm 5 ) \cdot 10^{6} \frac{kg}{s^2 m}$
Da der relative Fehler viel zu groß ist und der $T^2$-Achsenabschnitt auch ziemlich groß ist, ist dieser Wert für weitere Berechnungen nicht emphelenswert.
Messung 2 - Stab an Saite dick ($r = (1 \pm 0.025)mm$)
Anfangsbedingungen:
$\phi_0 = \pi, \dot{\phi}_0 = 0$
Unsicherheiten:
$ u(L) = 0,03m,$ $u(T_{10}) = 0,5s$
| Höhe $L/m$ | Periodendauer $T_{10}/s$ |
|---|---|
| 0.62 | 16.32 |
| 0.53 | 13.44 |
| 0.47 | 12.68 |
| 0.35 | 11.49 |
| 0.23 | 9.47 |
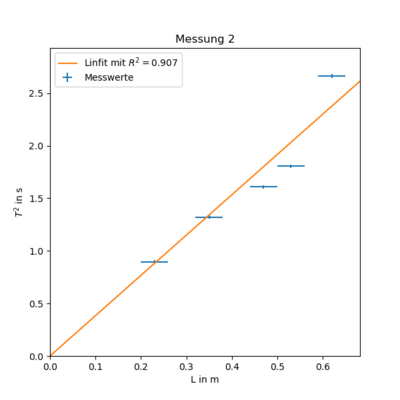
$ T(L)^2 = ( 383 \pm 20 ) \cdot 10^{-2} \frac{s^2}{m} \cdot L $
Aus der Theorie erwarten wir eine Steigung die sich aus $ st = \frac{I}{2 \pi^3 G r^4}$ zusammensetzt. Außerdem kennen wir schon $ I = (4,8 \pm 1,2) \cdot 10^{-5}\ kg\ m^2 $ und $ r = (1.0 \pm 0.025)mm \Longrightarrow r^4 = ( 100 \pm 10 ) \cdot 10^{-14} m^4 $. Nach Umstellen ergibt sich:
$ G = \frac{I}{2 \pi^3 \cdot st \cdot r^4 } = ( 20 \pm 6 ) \cdot 10^{4} \frac{kg}{s^2 m}$
Diese Berechnung ist im Vergleich zur ersten deutlich plausibler.
Messung 3 - Stab an Schnürsenkel ($r = (3 \pm 1)mm$)
Anfangsbedingungen:
$\phi_0 = 4 \cdot \pi, \dot{\phi}_0 = 0$
Unsicherheiten:
$ u(L) = 0,03m, u(T_{2}) = 0,5s$
Die Dämpfung ist hier groß. Deshalb messen wir 2 Perioden $T_2$ statt 10 Perioden $T_{10}$.
| Höhe $L/m$ | Periodendauer $T_{2}/s$ |
|---|---|
| 0,48 | 26,86 |
| 0,18 | 19,37 |
| 0,10 | 13,58 |
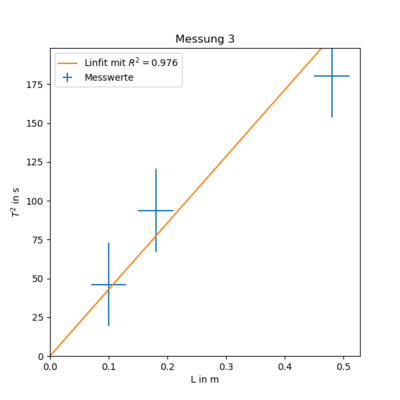
$ T(L)^2 = ( 43 \pm 4 ) \cdot 10^{1} \frac{s^2}{m} \cdot L $
Aus der Theorie erwarten wir eine Steigung die sich aus $ st = \frac{I}{2 \pi^3 G r^4}$ zusammensetzt. Außerdem kennen wir schon $ I = (4,8 \pm 1,2) \cdot 10^{-5}\ kg\ m^2 $ und $ r = (3 \pm 1)mm \Longrightarrow r^4 = ( 8 \pm 11 ) \cdot 10^{-11} m^4 $. Nach Umstellen ergibt sich:
$ G = \frac{I}{2 \pi^3 \cdot st \cdot r^4 } = ( 2 \pm 3 ) \cdot 10^{1} \frac{kg}{s^2 m}$
Diese Berechnung scheitert an der Annahme eines harmonischen Potentials.
Messung 4 - Topfdeckel 1 an Saite dick
Durchmesser $ d = (0.210 \pm 0.005) m $
Masse $ m = (0.07 + 0.65) kg $
Anfangsbedingungen:
$\phi_0 = \pi, \dot{\phi}_0 = 0$
Unsicherheiten:
$ u(L) = 0,03m, u(T_{3}) = 0,5s, u(m) = 0.03 kg$
| Höhe $L/m$ | Periodendauer $T_{3}/s$ |
|---|---|
| 0.56 | 38.88 |
| 0.29 | 27.11 |
| 0.17 | 20.57 |
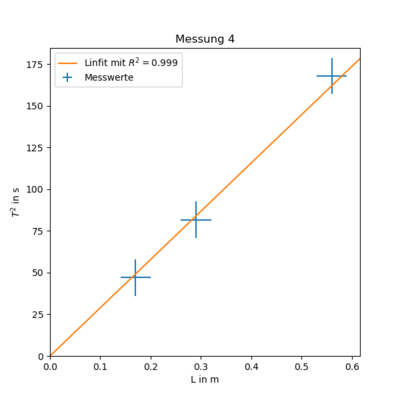
$ T(L)^2 = ( 290 \pm 7 ) \frac{s^2}{m} \cdot L $
Vergleicht man nun den Proportionalitätfaktor mit dem aus Messung 2 erhält man $ I_{Topf1}= \frac{st_{Topf1}}{st_{Stab}} \cdot I_{Stab} = ( 36 \pm 9 ) \cdot 10^{-4} \ kg\ m^2 $
Messung 5 - Topfdeckel 2 an Saite dick
Durchmesser $ d = (0.170 \pm 0.005) m $
Masse $ m = (0.07 + 0.05) kg $
Anfangsbedingungen:
$\phi_0 = \pi, \dot{\phi}_0 = 0$
Unsicherheiten:
$ u(L) = 0,03m, u(T_{5}) = 0,5s, u(m) = 0.03 kg $
| Höhe $L/m$ | Periodendauer $T_{5}/s$ |
|---|---|
| 0.50 | 26.69 |
| 0.33 | 21.36 |
| 0.17 | 14.51 |
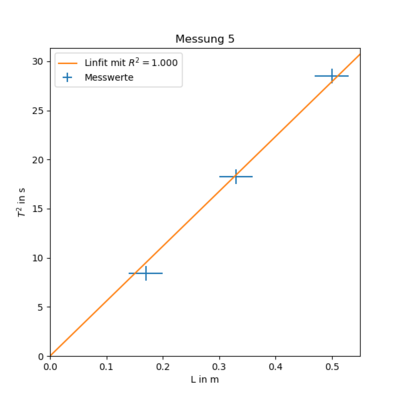
$ T(L)^2 = ( 558 \pm 15 ) \cdot 10^{-1}\frac{s^2}{m} \cdot L $
Vergleicht man nun den Proportionalitätfaktor mit dem aus Messung 2 erhält man $ I_{Topf_2}= \frac{st_{Topf_2}}{st_{Stab}} I_{Stab} = ( 70 \pm 18 ) \cdot 10^{-5} \ kg\ m^2 $
Auswertung
Für die zwei Topfdeckel erhalten wir
$ I_{Topf_1, Theorie} = 3,97 \cdot 10^{-3} \ kg\ m^2 \longleftrightarrow I_{Topf1, Experiment} = (3.7 \pm 1.1) 10^{-3} \ kg\ m^2 $
$ I_{Topf_2, Theoie} = 0,43 \cdot 10^{-3} \ kg\ m^2 \longleftrightarrow I_{Topf_2} = (0.71 \pm 0.22) 10^{-3} \ kg\ m^2 $
Wir sehen, dass wir für die höhere Masse im Fehlerintervall liegen. Bei höherer Masse ist möglicherweise das Modell des Torsionsmodules treffender und mögliche Störquellen weniger einflussreich.
Code zu den Plots
import numpy as np import matplotlib.pyplot as plt from scipy import stats from scipy.odr import * from help import string_correctly, err_evolution ul = 0.03 ut = 0.5 mess1 = {'val': np.array([[0.56, 17.5], [0.42, 15.9], [0.35, 15.6], [0.29, 12.9], [0.24, 12.58]]), 'phi': np.pi, 'nt': 10, 'r': 1 / 3 * 10 ** - 3, 'r_err': 0.1 / 3 * 10 ** - 3, 'i': 4.8 * 10 ** -5, 'i_err': 1.2 * 10 ** -5} mess2 = {'val': np.array([[0.53, 13.44], [0.62, 16.32], [0.47, 12.68], [0.35, 11.49], [0.23, 9.47]]), 'phi': np.pi, 'nt': 10, 'r': 1 * 10 ** - 3, 'r_err': 0.1 / 4 * 10 ** - 3, 'i': 4.8 * 10 ** -5, 'i_err': 1.2 * 10 ** -5} mess3 = {'val': np.array([[0.48, 26.86], [0.18, 19.37], [0.1, 13.58]]), 'phi': 4 * np.pi, 'nt': 2, 'r': 3 * 10 ** - 3, 'r_err': 1 * 10 ** - 3, 'i': 4.8 * 10 ** -5, 'i_err': 1.2 * 10 ** -5} mess4 = {'val': np.array([[0.56, 38.88], [0.29, 27.11], [0.17, 20.57]]), 'phi': np.pi, 'nt': 3, 'r': 1 * 10 ** - 3, 'r_err': 0.1 / 4 * 10 ** - 3, 'i': 4.8 * 10 ** -5, 'i_err': 1.2 * 10 ** -5} mess5 = {'val': np.array([[0.50, 26.69], [0.33, 21.36], [0.17, 14.51]]), 'phi': np.pi, 'nt': 5, 'r': 1 * 10 ** - 3, 'r_err': 0.1 / 4 * 10 ** - 3, 'i': 4.8 * 10 ** -5, 'i_err': 1.2 * 10 ** -5} def lin(a, x): return a * x def r_4(r): return r ** 4 def torsion(i, r4, slope): return i / (2 * np.pi ** 3 * r4 * slope) def trägmom(i2, slope1, slope2): return i2 * slope1 / slope2 messes = [mess1, mess2, mess3, mess4, mess5] for j in range(len(messes)): mess = messes[j] vals = np.transpose(mess['val']) nt = mess['nt'] lengths = vals[0] l_max = max(lengths) l_mean = sum(lengths) / len(lengths) lens = np.linspace(0, 1.1 * l_max, num=50) times = [vals[1][i] / nt for i in range(len(vals[1]))] t_quad = [times[i] ** 2 for i in range(len(times))] tq_max = max(t_quad) tq_mean = sum(t_quad) / len(t_quad) uts = [2 * tq * ut / (nt ** 2) for tq in t_quad] sol = stats.linregress(lengths[:len(t_quad)], t_quad) lin_model = Model(lin) data = RealData(lengths[:len(t_quad)], t_quad, sx=ul, sy=uts) sol_real = ODR(data, lin_model, beta0=[1.]).run() fit = [sol_real.beta[0] * l for l in lens] dls = [l - l_mean for l in lengths] sdl = sum([abs(dl) for dl in dls]) / len(dls) dtqs = [tq - tq_mean for tq in t_quad] sdtq = sum([abs(dtq) for dtq in dtqs]) / len(dtqs) covltq = sum([dls[i] * dtqs[i] for i in range(len(dls))]) / (len(dls) - 1) corltq = covltq / (sdl * sdtq) fig = plt.figure(figsize=(6, 6)) ax = fig.add_subplot(111) ax.errorbar(lengths, [time ** 2 for time in times], linestyle='', marker='', xerr=ul, yerr=2 * tq_mean * ut / (nt ** 2), label='Messwerte') ax.plot(lens, fit, linestyle='-', label='Linfit mit $R^2 =$' + "%.3f" % (round(sol.rvalue ** 2, 3))) ax.set_xlim(0, 1.1 * l_max) ax.set_ylim(0, 1.1 * tq_max) ax.set_title('Messung ' + str(j + 1)) ax.set_xlabel('L in m') ax.set_ylabel('$T^2$ in s') ax.legend() plt.savefig('Drehschwingung.Messung' + str(j + 1) + '.png') plt.show() slope = sol_real.beta[0] slope_err = sol_real.sd_beta[0] print(j + 1, ':') print('Slope: ', string_correctly(slope, slope_err)) if j < 3: r = mess['r'] r_err = mess['r_err'] i = mess['i'] i_err = mess['i_err'] if j == 1: i2 = i i2_err = i_err slope2 = slope slope2_err = slope_err r4, r4_err = err_evolution(r_4, [r], [r_err]) g, g_err = err_evolution(torsion, [i, r4, slope], [i_err, r4_err, slope_err]) print('r^4: ', string_correctly(r4, r4_err)) print('g: ', string_correctly(g, g_err), end='\n\n\n') else: i, i_err = err_evolution(trägmom, [i2, slope, slope2], [i2_err, slope_err, slope2_err]) print('I: ', string_correctly(i, i_err), end='\n\n\n')
Hilfscode
def round_correctly(val, err): first_sign = 0 while err // (10 ** first_sign) > 0: first_sign += 1 while err // (10 ** first_sign) == 0: first_sign -= 1 if err // (10 ** first_sign) < 3: first_sign -= 1 return round(val * 10 ** -first_sign), round(err * 10 ** -first_sign), first_sign def lin_fit_label(sol, xstr): return '$Fit = ' + string_correctly(sol.slope, sol.stderr) + ' \\cdot ' + xstr + ' + ' + string_correctly( sol.intercept, sol.intercept_stderr) + '$; $R^2 = ' + str(round(sol.rvalue ** 2, 3)) + '$' def string_correctly(val, err): val, err, pot = round_correctly(val, err) return ' ( ' + str(int(val)) + ' \pm ' + str(int(err)) + ' )' + (' \\cdot 10^{' + str(pot) + '} ') * (pot != 0) def err_evolution(func, params, errors): val = func(*params) err_q = 0 for i in range(len(params)): _, _, pot = round_correctly(params[i], errors[i]) h = 10 ** (pot - 5) upper = (params[j] + h * (j == i) for j in range(len(params))) lower = (params[j] - h * (j == i) for j in range(len(params))) diff = (func(*upper) - func(*lower)) / (2 * h) err_q += (diff * errors[i]) ** 2 return val, err_q ** 0.5


