meta data for this page
Gruppe 314 - Drehschwingungen
Eine Web-Site gestaltet von Zoe Lohmann und Lisa Digiacomo zur Protokollierung des Versuchs 'Drehschwingungen'.
Theoretische Grundlagen
Bevor das eigentliche Experimentieren losgeht, sollte man sich die theoretischen Grundlagen anschauen, um die Ergebnisse interpretieren zu können. Dazu werden Fragen und Aufgaben bearbeitet.
Allgemeiner Versuchsaufbau
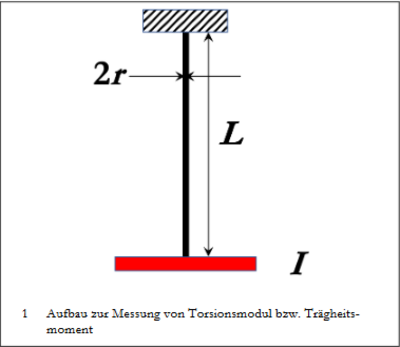
(Quelle: Aufgabenstellung Drehschwingung ©2020 R. Scholz, K.-M.Knaak und K.Weber, LUH)
Wird ein Draht mit einem anhängenden Körper um dem Winkel $\varphi$ aus seiner Ruhelage gelenkt, so wirkt ein rücktreibendes Drehmoment $D = - D_{R} \cdot \varphi $ mit $D_{R}$ einer Winkelrichtgröße abhängig von Material und dessen Abmessungen.
Die Bewegungsgleichung $I \cdot \frac{d^2 \varphi}{d t ^2} = -D _{R}\cdot \varphi$ für diesen Aufbau hat die Lösung $\varphi (t) = \varphi_{0} \cdot \cos{(\omega t)}$ mit $\omega = \sqrt{\frac{D_{R}}{I}}$ ($\omega$ der Kreisfrequenz der Bewegung).
Berechnung der Schwingungsdauer T
Nun soll aus der Kreisfrequenz $\omega$ die Schwingungsdauer T bestimmt werden. Dazu hilft die Beziehung $\omega = \frac{2 \pi}{T}$. Diese kann man der Kreisfrequenz aus der Lösung der Bewegungsgleichung gleichgesetzt werden und wir erhalten:
$\sqrt{\frac{D_{R}}{I}} = \frac {2\pi}{T} \leftrightarrow T = 2\pi \cdot \sqrt{\frac{I}{D_{R}}}$
Berechnungen vom rücktreibenden Drehmoment $D $
Das rücktreibende Drehmoment ist stark von dem Radius des verwendetenen Materials.
Mit Hilfe der Formel $ D_{R} = \frac{\pi }{ 2} \cdot \frac{G \cdot R^4}{L}$ mit G dem Torsionsmoduls des Materials, R dem Radius und L der Länge des Drahtes.
Als Beispiel wurde ein Kupferdraht verwendet. Dieser hat ein Torsionsmodul von $G = 47~ GPa = 47^{9}~ Pa$. Die Länge wurde auf $L = 20 ~cm$ gesetzt. Für verschiedene Drahtradien $R_{i}$ wurden folgende rücktreibende Drehmomente $D = - D_{R} \cdot \varphi $ für einen konstanten Winkel von $\varphi = 0,25 ~rad$ berechnet:
$R_{1} = 2 ~mm$: $D_{R_{1}} = \frac{\pi \cdot 47^{9}~Pa \cdot (0,02~m)^{4}}{2\cdot 0,2 m}= 59061,94 ~ \frac{Nm}{rad} \leftrightarrow D= -14765,49 ~Nm$
$R_{2} = 3 ~mm$: $D_{R_{1}} = \frac{\pi \cdot 47^{9}~Pa \cdot (0,03~m)^{4}}{2\cdot 0,2 m}= 299001,08 ~ \frac{Nm}{rad}\leftrightarrow D= -74750,27 ~Nm$
$R_{3} = 2,5~ mm$: $D_{R_{1}} = \frac{\pi \cdot 47^{9}~Pa \cdot (0,025~m)^{4}}{2\cdot 0,2 m}= 144194,19 ~ \frac{Nm}{rad}\leftrightarrow D= -36048,55 ~Nm$
$R_{4} = 2,1 ~mm$: $D_{R_{1}} = \frac{\pi \cdot 47^{9}~Pa \cdot (0,021~m)^{4}}{2\cdot 0,2 m}= 71790,16 ~ \frac{Nm}{rad}\leftrightarrow D= -17947,54 ~Nm$
Man kann erkennen, das eine kleine Änderung von $\Delta R = 0,1 ~ mm$ ausreicht, dass sich $D$ betragsmäßig um knapp $22 \% $ erhöht.
Anfangsbedingungen zur Bestimmung der Lösung der Bewegungsgleichung
Um die Lösung der Bewegungsgleichung zu erhalten, müssen Anfangsbedinungen gestellt werden. Diese lauten :
$\varphi (0) = \varphi_{0}$, $\frac{d \varphi}{dt} = 0$ und $\frac{d ^2\varphi}{dt^2} = -\varphi_{0} \cdot \frac{D_{R}}{I}$.
Um diese zu beweisen, werden diese in die Lösung eingesetzt:
$\varphi (0) = \varphi_{0} \cdot \cos{(\omega \cdot0)}= \varphi_{0} \cdot 1 = \varphi_{0}$
Die erste Bedinung ist erfüllt.
Für die weiteren müssen die Ableitungen der Lösung gebildet werden:
$\frac{d \varphi(t)}{dt}= - \varphi_{0} \cdot \omega \cdot \sin{(\omega t)}$
$\frac{d^2 \varphi(t)}{dt^2}= - \varphi_{0} \cdot \omega^2 \cdot \cos{(\omega t)}$
Jetzt kann man die Ableitungen zur Zeit $t=0$ berechenen:
$\frac{d \varphi(0)}{dt}= - \varphi_{0} \cdot \omega \cdot \sin{(\omega \cdot 0)}= 0$
$\frac{d^2 \varphi(0)}{dt^2}= - \varphi_{0} \cdot \omega^2 \cdot \cos{(\omega \cdot 0)}= -\varphi_{0}\cdot \omega ^2=-\varphi_{0}\cdot\frac{D_{R}}{I}$
Damit sind auch diese Bedingen erfüllt.
Einheiten wichtiger Größen
Gefragt wird, welche Einheiten jeweils $D$, $D_{R}$, $I$ und $\varphi$ haben.
Die Winkelrichtgröße $D_{R}$ hat die Einheit $[\frac{Nm}{rad}]$. Sie ist eine Propotionalitätskonstante zwischen Drehmoment und Drehwinkel.
Das Drehmoment $D$ hat die Einheit $[Nm]$. Es ist das Produkt aus Armlänge $r$ und an dieser angreifenden Kraft $F$.
Das Trägheitsmoment $I$ hat die Einheit $[kgm^2]$. Es ist das Produkt aus Masse $m$ des Körpers und dem Quadrat des Radius $r$ zur Drehachse.
Der Winkel $\varphi$ hat die Einheit $[rad]$. Radiant ist ein Winkelmaß, das den entsprechenden Winkel als Länge im Einheitskreis angibt.
Beweis von $\omega$
Für den Beweis von $\omega$ soll die Gleichung $\varphi (t) = \varphi_{0} \cdot \cos{(\omega t)}$ und deren zweite Ableitung in $I \cdot \frac{d^2 \varphi}{d t ^2} = -D _{R}\cdot \varphi$ eingesetzt werden:
$-I \cdot \varphi_{0} \cdot \omega^2 \cdot \cos{(\omega t)} = -D _{R}\cdot \varphi_{0} \cdot \cos{(\omega t)}~~~~~~$| : $\varphi_{0}$
$-I \cdot \omega^2 \cdot \cos{(\omega t)} = -D _{R} \cdot \cos{(\omega t)}~~~~~~$| $+D _{R} \cdot \cos{(\omega t)}$
$-I \cdot \omega^2 +D _{R} \cdot (\cdot \cos{(\omega t)}) = 0~~~~~~$
Damit für variable $t$ diese Gleichung erfüllt ist, muss $-I \cdot \omega^2 +D _{R}$ Null sein.
$-I \cdot \omega^2 +D _{R}= 0~~~~~~$|$-D_{R} ~ $| : $- I$
$\omega^2 = \frac {D_{R}}{I}~~~~~~$|√
$\Rightarrow \omega = \sqrt{\frac{D_{R}}{I}}$
Experimentelle Bestimmung des Drehmoments
Das Drehmoment kann man mit einem Drehmomentschlüssel bestimmt werden. Dabei verbiegt sich der lange Schaft mit dem Griff bei Einwirkung einer Kraft. Die Stellung des Zeigers verändert sich dabei nicht. An einer Skala kann da das Drehmoment abgelesen werden.
Zum anderen kann man das Drehmoment über den Drehimpuls bestimmen. Der Drehimpuls ist das Produkt aus Winkelgeschwingigkeit und Trägheitsmoment. Beides kann experimentell bestimmt werden und mit der Beziehung, dass das Drehmoment die zeitliche Änderung des Drehimpulses ist, das Drehmoment berechnen.
Rotationsenergie
Arbeit ist bei Translation das Produkt aus Kraft und Weg. In der Rotation ist das Drehmoment und der Drehwinkel das Äquivalent zu Kraft und Weg. Das bedeutet, dass die Änderung der Arbeit durch das Produkt aus Drehmoment und der Änderung des Winkels ausgedrückt werden kann. In der Translation wäre die Änderung der Arbeit das Produkt aus Arbeit und Änderung des Ortes.
$dW = D \cdot d\varphi$.
Jedes Masseelement eines rotierenden starren Körper besitzt eine bestimmte kinetische Energie, die von der Masse und deren Geschwindigkeit abhängig ist. Die Geschwindigkeit hängt bei Winkelgeschwindigkeit vom Abstand von der Drehachse ab. Diese Energie bezeichnet man als Rotationsenergie:
$E_{Rot}=\frac{1}{2}\cdot I\cdot\omega^2$
Steiner'sche Satz
Der Steiner'sche Satz besagt, dass wenn ein Körper der Masse $m$ um eine Achse rotiert, die im Abstand $h$ parallel zur Schwerpunktsachse des Körpers verläuft, so muss zum jeweiligen Wert des Trägheitsmoments der Term $m\cdot h^2$ addiert werden. Es folgt:
$I = I_{s} + m\cdot h^2$.
Um den Steiner´schen Satz experimentell zu beweisen, benutzt man einen Drehscheiben-Torsionspendel.
Torsionsmodul des Drahtes
Versuchsaufbau
Im Folgeden Bild ist der Versuchsaufbau gezeigt:

Es wurde eine Plastikrolle verwendet, die an einem Stahldraht hängt. Der Stahldraht hängt an einer Lampe, damit sich die Rolle frei drehen kann.
Der Drehwinkel, bei dem die Rolle gedreht wurde, um damit die Schwingungsdauer zu bestimmen, wurde wie folgt bestimmt:
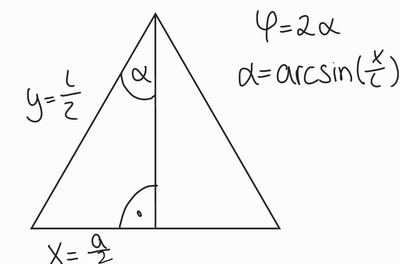
Die Auslenkung wurde für alle Messungen konstant bei $a= (4,00\pm 0,05)~cm$ gehalten. Die Länge der Rolle ist hier $l= ( 9,80 \pm 0,05)~cm$. Somit ergab sich ein Winkel $\varphi = 0,841~ rad $.
Fehler des Winkels
$u(\varphi) = \sqrt{(\frac{\partial \varphi}{\partial x}\cdot u(x))^2 + (\frac {\partial \varphi}{\partial y}\cdot u(y))^2}$
$u(\varphi) = \sqrt{(\frac{1}{y\cdot \sqrt{1-(\frac{x}{y})^2}}\cdot u(x))^2 + (-\frac {x}{y^2 \cdot sqrt{1-(\frac{x}{y})^2}}\cdot u(y))^2}$
$u(\varphi) = 0,0123~ rad$
Der Drehwinkel ist somit $\varphi = (0,841 \pm 0,123)~rad$.
Als anhängender Körper wurde eine Rolle benutzt. Dessen Maße sind :
Masse der Rolle $m = (30,0 \pm 0,5)~g$, Länge der Rolle $l=(9,80 \pm 0,05)~cm$ und Radius der Rolle $R = (4,80\pm 0,05)~cm$.
Mit
$I=\frac{1}{4}\cdot m\cdot R^2 + \frac{1}{12}\cdot m\cdot l^2$
kann dessen Trägheitsmoment berechnet werden : $ I = 0,0000413~ kgm^2$.
Mit Hilfe der Gaußschen Fehlerfortpflanzung:
$u(I)=\sqrt{2\cdot ((\frac{R^2}{4}+\frac{l^2}{12})\cdot u(m))^2 + (\frac {1}{2}\cdot m\cdot R \cdot u(R))^2+(\frac{1}{6}\cdot m\cdot l\cdot u(l))^2}$.
erhält man : $I = (4,13 \pm 0,11)\cdot 10 ^{-5} kgm^2$.
Messwerte Gitarrenseite
Die Messwerte werden mit Abzug von der Schrecksekunde $0,291~s$ (s. Messunsicherheiten) angegeben.
| L in m | $4~T$ in s | T in s | Standardabweichung in s | Standardfehler in s |
|---|---|---|---|---|
| 0,365 | 14,80 | 3,69 | 0,05 | 0,02 |
| 14,77 | ||||
| 14,70 | ||||
| 15,01 | ||||
| 14,46 | ||||
| 0,298 | 13,51 | 3,349 | 0,03 | 0,013 |
| 13,39 | ||||
| 13,20 | ||||
| 13,46 | ||||
| 13,43 | ||||
| 0,243 | 12,14 | 3,030 | 0,02 | 0,012 |
| 11,99 | ||||
| 12,27 | ||||
| 12,04 | ||||
| 12,16 | ||||
| 0,158 | 9,80 | 2,435 | 0,02 | 0,009 |
| 9,62 | ||||
| 9,77 | ||||
| 9,81 | ||||
| 9,71 | ||||
| 0,089 | 7,45 | 1,885 | 0,017 | 0,007 |
| 7,57 | ||||
| 7,49 | ||||
| 7,60 | ||||
| 7,59 |
Messwerte Gummiband
| L in m | T in s | Mittelwert in s | Standardabweichung in s | Standardabweichung in s |
|---|---|---|---|---|
| 0,137 | 8,61 | 8,52 | 0,06 | 0,03 |
| 8,48 | ||||
| 8,46 | ||||
| 8,54 | ||||
| 8,53 | ||||
| 0,094 | 6,39 | 6,15 | 0,15 | 0,07 |
| 6,18 | ||||
| 6,01 | ||||
| 6,08 | ||||
| 6,10 | ||||
| 0,034 | 3,12 | 3,16 | 0,04 | 0,02 |
| 3,22 | ||||
| 3,14 | ||||
| 3,13 | ||||
| 3,18 |
Messwerte Kabel
| L in m | T in s | Mittelwert in s | Standardabweichung in s | Standardfehler in s |
|---|---|---|---|---|
| 0,964 | 0,477 | 0,485 | 0,014 | 0,006 |
| 0,507 | ||||
| 0,472 | ||||
| 0,480 | ||||
| 0,487 | ||||
| 0,588 | 0,410 | 0,401 | 0,012 | 0,005 |
| 0,407 | ||||
| 0,382 | ||||
| 0,397 | ||||
| 0,410 | ||||
| 0,221 | 0,210 | 0,217 | 0,009 | 0,004 |
| 0,207 | ||||
| 0,225 | ||||
| 0,227 | ||||
| 0,217 |
Messwerte Garn
| L in m | T in s | Mittelwert in s | Standardabweichung in s | Standardfehler in s |
|---|---|---|---|---|
| 0,756 | 9,82 | 9,60 | 0,3 | 0,13 |
| 9,57 | ||||
| 9,20 | ||||
| 9,78 | ||||
| 9,63 | ||||
| 0,532 | 7,16 | 7,25 | 0,09 | 0,04 |
| 7,29 | ||||
| 7,27 | ||||
| 7,36 | ||||
| 7,17 | ||||
| 0,108 | 3,595 | 3,61 | 0,04 | 0,018 |
| 3,660 | ||||
| 3,615 | ||||
| 3,550 | ||||
| 3,630 |
Berechnung des Torsionsmoduls G
Zur Berechnung des Torsionsmoduls werden die Gleichungen $D_{R} = \frac{\pi}{2} \cdot \frac{G \cdot r^4}{L}$ und $ T= 2\cdot \pi \sqrt{\frac {I}{D_{R}}}$ verwendet. Wenn wir die Gleichung für die Schwingungsdauer nach $D_{R}$ umstellen, können wir beides gleichsetzen und erhalten
$ G = \frac{8\pi \cdot I \cdot L}{T^2 \cdot r^4}$.
Aus der Steigung der Graphen in der Auswertung kann man $\frac{T^2}{L}$ ablesen. Den Rest der Gleichung sind bekannte Größen, die man dann einsetzen kann und erhält das Torsionsmodul. Das Trägheitsmoment der Rolle ist $I = (0,0000413 \pm 0,0000011) ~kgm^2$.
Die Unsicherheit für dieses Torsionsmodul lässt sich wie folgt mit der Gauß'schen Fehlerfortpflanzung berechen (a ist hierbei die Steigung der Linearen Regression):
$u(G)=\sqrt{(-\frac{1}{a^2}\cdot\frac{8\pi \cdot I}{r^4}\cdot u(a))^2+ (\frac{1}{a}\cdot\frac{8\pi}{r^4}\cdot u(I))^2+(\frac{1}{a}\cdot\frac{32\pi\cdot I}{r^5}\cdot u(r))^2}$.
Torsionsmodul der Gitarrensaite
Die Steigung des Graphens für die Gitarrensaite ist $a = (36,3 \pm 0,7 )~\frac{m}{s^2}$ und $ r = (0,00014 \pm 0,00005)~m$.
$ G_{Saite} = ( 74,4 \pm 2,4)~ GPa$.
Der Literaturwert für Stahl ist etwa $G = 79,3 ~GPa$. Das ist eine Abweichung von $6,6\%$, was anhand der Messunsicherheiten erklärbar sein wird.
Torsionsmodul des Gummiband
Die Steigung des Graphens für das Gummiband ist $a = (601,4 \pm 75,6 )~\frac{m}{s^2}$ und $ r = (0,0005 \pm 0,00005)~m$.
$ G_{Gummi} = ( 0,0276\pm 0.0111)~ GPa$.
Der Literaturwert beträgt etwa $0,0003~GPa$. Es muss also bei der Messung ein Fehler aufgetreten sein, oder bei der Berechung von dem Torsionsmodul, da sich der Wert um $10^2$ vergrößert hat.
Torsionsmodul des Kabels
Die Steigung des Graphens für das Kabel ist $a = (0,25 \pm 0,03 )~\frac{m}{s^2}$ und $ r = (0,0015 \pm 0,00005)~m$.
$ G_{Kabel} = ( 0,82\pm 0,15)~ GPa$.
Torsionsmodul des Garns
Die Steigung des Graphens für das Garnstück ist $a = (118,2 \pm 21,2 )~\frac{m}{s^2}$ und $ r = (0,001 \pm 0,00005)~m$.
$ G_{Garn} = ( 0,009 \pm 0,002) ~GPa$.
Leider wurden für die zwei weiteren Torsionsaufhängungen keine Literaturwerte gefunden.
Berechnung des Trägheitsmoments
Versuchsaufbau
Um das Trägheitsmoment zu bestimmen, brauchen wir die Periodendauer T. Diese haben wir bestimmt, indem wir für fünf Perioden die Zeit gestoppt haben. Für eine Periode die Zeit zu messen, wäre die Unsicherheit noch viel größer. Außerdem haben wir dies fünfmal gemacht und daraus den Mittelwert durch fünf geteilt. Zum stoppen der Zeit haben wir die Akustische Stoppuhr von phyphox genutzt. Für alle Messungen haben wir einen Auslenkungswinkel von 15° bestimmt. Diesen haben wir mit einem Geodreieck gemessen.
Das Trägheitsmoment haben wir mit der Folgenden Formel berechnet:
$De=\frac{π}{2}·\frac{G·r^4}{l}$
$T=2π·\sqrt{\frac{I}{D_R}}$
$T^2=4π^2·\frac{I}{D_R}$
$D_R=4π^2·\frac{I}{T^2}$
$\frac{π}{2}·\frac{G·r^4}{l}=4π^2·\frac{I}{T^2}$
$\frac{G·r^4}{l}=8π·\frac{I}{T^2}$
$I=\frac{T^2}{8π}·\frac{G·r^4}{l}$
Für die Bestimmung der Periodendauer T hab ich drei Gegenstände benutzt. Die Gitarrensaite habe ich an einer frei hängenden Lampe befestigt (siehe Foto). Die Länge betrug dabei $l=0,63 ~m$. Den Radius der genutzten Saite haben wir auf $r = (0,00015\pm 0,00005)~ m$ angenommen (Gitarrensaite hat laut Wikipedia etwa 0.012 Zoll) . Für das Torsionsmodul haben wir mit dem Literaturwert von $G=79,5 ~GPa$ gerechnet, um weitere Fehler zu vermeiden.
Damit die Perdiodendauer genauer ist, haben wir unsere Reaktionszeit gemessen und diese von der Periodendauer abgezogen. Die gemittelte Reaktionszeit betrug $<T>=0,33855~ s$. Diese ist beim berechneten Trägheitmoment bereits berücksichtigt. Die Länge des Drahtes war konstant bei $l = (63,00 \pm 0,05)~cm$. Die Unsicherheit der Schwingungsdauer wurde jeweils mit dem Standardfehler bestimmt.
Für die DVD-Schachtel ergaben sich folgende Messwerte:
| T in s (für 5 Perioden) | T in s (für eine Periode) |
|---|---|
| 7,779 | 1,5558 |
| 8,051 | 1,6102 |
| 8,028 | 1,6056 |
| 8,089 | 1,6178 |
| 7,541 | 1,5082 |
Es ergibt sich eine Periodendauer von $<T>_{1} = 1,24097 ~s$.
Die DVD-Schachtel hat eine Masse von $m_{1} = 0,155 ~kg$.
Die Unsicherheit der Schwingungsdauer beträgt $u(T) = 0,02~s$.
Damit haben wir für die DVD-Schachtel ein Trägheitsmoment von
$I_{1} = 1,8361\cdot 10^{-5}~kg·m^2$.
Die zweite Messung haben wir mit einer Aludose durchgeführt. Dabei ergaben sich folgende Messwerte:
| T in s (für 5 Perdioden) | T in s (für eine Periode) |
|---|---|
| 8,232 | 1,6464 |
| 8,003 | 1,6006 |
| 8,008 | 1,6016 |
| 7,939 | 1,5878 |
| 7,998 | 1,5996 |
Daraus ergibt sich eine Periodendauer von $<T>_{2} = 1,26865 ~s$.
Die Dose hatte eine Masse von $m_{2} = 0,045 ~kg$.
Die Unsicherheit ist hier $u(T) = 0,0101 ~s$.
Damit haben wir für die Aludose ein Trägheitsmoment von
$I_{2} = 1,904\cdot 10^{-5}~kg·m^2$
Die letzte Messung haben wir mit einer mit Wasser gefüllten Christbaumkugel durchgeführt. Dabei ergaben sich folgende Messwerte:
| T in s (für 5 Perdioden) | T in s (für eine Periode) |
|---|---|
| 7,968 | 1,5936 |
| 7,915 | 1,583 |
| 7,868 | 1,5736 |
| 8,004 | 1,6008 |
| 8,094 | 1,6188 |
Daraus ergibt sich eine Perdiodendauer von $<T>_{3} = 1,25541 ~s$.
Die Masse beträgt $m_{3} = 0,092 ~kg$.
Die Unsicherheit ist hier $u(T) = 0,008 ~s $.
Wir berechnen für die Christbaumkugel ein Trägheitsmoment von $I_{3} = 1,8714\cdot 10^{-5}~kg·m^2$.
Messunsicherheit des Trägheitsmoments
Die Unsicherheit des Trägheitsmoments lässt sich wie folgt mit der Gaußschen Fehlerfortpflanzung bestimmen:
$u(I) = \sqrt{(\frac{T\cdot G \cdot r^4}{4\pi\cdot l}\cdot u(T))^2+(\frac{T^2 \cdot G\cdot r^3}{2\pi \cdot l}\cdot u(r))^2+(-\frac{T^2\cdot G\cdot r^4}{8\pi \cdot l^2}\cdot u(l))^2}$
Es ergeben sich die Trägheitsmomente
$I_{1}= (0,000018\pm 0,000007) ~kgm^2$,
$I_{1}= (0,000019\pm 0,000008) ~kgm^2$,
$I_{1}= (0,000019\pm 0,000008) ~kgm^2$.
Messunsicherheiten
Schrecksekunde für Experiment 1
Die Schrecksekunde ist eine Unsicherheit bei der Messung von Zeit mit einer Stoppuhr. Hier wird die Schrecksekunde durch ein Reaktionszeit-Test ermittelt. Dort wird die eigene Reaktionszeit ermittelt, die man hat, wenn ein Ereignis eintritt und man darauf reagieren muss.
Nach 20 Messungen wurde ein Mittelwert von $0,291~s$ ermittelt, die von jeder Messung abgezogen wird.


