meta data for this page
This is an old revision of the document!
Besenstiel -- gruppe352
Der Versuch wurde durchgeführt von: Marius Burgath
Die Wiki-Seite wurde angelegt am: 17 December 2020 22:17
Anmerkung: Mein Gruppenpartner ist abgesprungen - Herr Weber wurde bereits benachrichtigt. Bisher hat sich noch kein neuer Gruppenpartner finden können, weshalb ich den Versuch alleine durchführe und entsprechend auch dieses “Wiki-Logbuch” alleine bearbeite.
Einleitung
In diesem “Wiki-Logbuch” dokumentiere ich meine Versuchsdurchführung bzw. meinen Versuchsaufbau zum “kippenden Besenstiel”. Zuerst wird das Computerprogramm vorgestellt, das bei der Aufgabe “numerische Lösung” erstellt werden soll. Programmiert habe ich dieses mit Mathematica. Anschließend wird mein Versuchsaufbau vorgestellt (verwendete Materialien, konkrete Durchführung,…) und das auch mit einigen Bildern belegt. Der letzte Teil dieses “Wiki-Logbuchs” sind meine aufgenommenen Messwerte, die ich dann in dem eigentlichen Versuchsbericht auswerte.
Computerprogramm
Als Programm zur Lösung der DGL nutze ich Mathematica. Dafür implementiere ich das Zeitschrittverfahren zunächst selbst und nutze anschließend noch eine von Mathematica eingebaute, interne Funktion.
1.) Numerische Lösung mit dem Zeitschrittverfahren ohne NDSolve
Die DGL $\ddot{\phi} = \frac{3 g \cdot sin(\phi)}{2 l} $ soll mit dem Zeitschrittverfahren gelöst werden. Beim Zeitschrittverfahren wird in einer ersten Näherung zu einem kleinen Zeitschritt $\Delta$t =: h nach der Anfangszeit t = 0 genähert, also $\dot{\phi}(\Delta t) = \dot{\phi}(0) + \Delta t \cdot \ddot{\phi}(0)$ sowie $\phi(\Delta t) = \phi_0 + \Delta t \cdot \dot{\phi}(\Delta t)$. Dabei lässt sich $\ddot{\phi}(0)$ aus der DGL $\ddot{\phi}(0) = \frac{3 g \cdot sin(\phi_0)}{2 l} $ ermitteln.Dies lässt sich dann weiter fortsetzen, da man bei der ersten Näherung “lokal” eine Lösung bzw. einen Näherungswert erhalten hat und diese dann wieder einsetzen kann. So lässt sich für die höhere Näherung allgemein $\dot{\phi}(t+\Delta t) = \dot{\phi}(t) + \Delta t \cdot \ddot{\phi}(t)$ und damit dann $\phi(t+\Delta t) = \phi (t) + \Delta t \cdot \dot{\phi}(t+\Delta t)$ ansetzen. Dies kann immer weiter durchgeführt werden, also für immer mehr Zeitschritte $\Delta t$, sodass man zuerst eine Näherung von $\phi (\Delta t)$ erhält, dann von $\phi (2\Delta t)$ usw.. Genauer ist das Verfahren, je kleiner die gewählten Zeitschritte $\Delta$t =: h sind. Das hier genutzte Verfahren wird allgemein als “Euler-Verfahren” bezeichnet und ist eine Möglichkeit, numerische Ausdrücke für die Lösungen von Differentialgleichungen zu erhalten.
Für Mathematica definiere ich zuerst mit der Funktion “euler” einen solchen allgemeinen Eulerschritt. Im Folgenden wird dafür $\phi$ als x bezeichnet und $ \dot{\phi}$ als v, um später Verwechslungen zu vermeiden. Die von mir definierte Funktion “euler” liefert also aus dem “Anfangstripel” {${t_0, \phi_0, \dot{\phi_0}}$} ein neues, genähertes Tripel nach dem Zeitschritt $\Delta$t =: h . Dies wird dann wieder eingesetzt und das Verfahren somit wiederholt, um genäherte Lösungen für größere Zeiten zu erhalten. Dafür, dass die neuen Näherungen immer wieder eingesetzt werden, sorgt der in Mathematica eingebaute praktische Befehl “Nest”. Mit der Variablen n kann dann die Anzahl der auszuführenden Zeitschritte $\Delta$t =: h , also auch die Anzahl der Wiederholungen des Verfahrens, angegeben werden.
Meine Definitionen hängen zudem allgemein von den Zeitschritten $\Delta$t =: h sowie der Länge l des verwendeten Stiels ab, damit das Programm dann bequem für andere Parameter genutzt werden kann, indem für l und $\Delta$t dann einfach konkrete Werte eingesetzt werden. Der Mathematica - Programmcode für die Definitionen ist:
f[{t_,x_,v_}]:=v
g[{t_,x_,v_},l_]:= Sin[x]* (3*9.81/(2*l))
euler[{t_,x_,v_},h_,l_]:={t+h, x+h* f[{t,x,v}],v+h* g[{t,x,v},l]}
Euler[n_,x0_,h_,l_]:=Nest[euler[#1,h,l]&,{0,x0,0},n]
So kann bspw. eine hundertmalige Wiederholung des Verfahrens bei einem Zeitschritt von $\Delta$t = 1/100 s = 10 ms sowie einer Stablänge von l = 1,45 m und einem Anfangswinkel von $x_0:= \phi_0$ = 0,25 rad ausgeführt werden, indem einfach die entsprechenden Argumente für die Funktion “Euler” gewählt werden:
Euler[100,0.25,1/100,1.45]
Als Output liefert Mathematica für diese konkreten Argumente das Tripel {1, 2.49478, 6.03056}. Der zweite Eintrag aus dieser Liste gibt den Winkel $\phi$ an. Im Folgenden definiere ich also eine Funktion, die genau diesen zweiten Eintrag des Tripels “extrahiert”, um anschließend damit arbeiten zu können:
phineu[n_,x0_,h_,l_]:=Part[Euler[n,x0,h,l],2]
Das Programm lässt sich mit Abb. 3 vom Aufgabenblatt prüfen. In dieser ist zu erkennen, dass bei l = 1,45 und $\phi$ = 0,25 rad sowie einem Zeitschritt von $\Delta$ t = 1/100 s = 10 ms die Fallzeit in etwa 0,82 s beträgt. Fallzeit bedeutet, dass nach dieser Zeit der Winkel von $\phi$ = $\pi$/2 rad erreicht wird und der Stab somit auf dem Boden liegt. Nur bis zu diesem Endwinkel ist also das Verfahren relevant, da der Stab auf den Boden trifft und es somit im physikalischen Zusammenhang gesehen bei den durchgeführten Experimenten keine größeren Winkel als $\pi$/2 rad gibt. Die Fallzeit von T = 0,82 s beträgt dann etwa $82 \cdot \Delta$t = 82/100 s , das entspricht also einer 82-maligen Durchführung des obigen Verfahrens (n = 82). Mit dem obigen Verfahren lässt sich entsprechend ermitteln:
phineu[82,0.25,1/100,1.45]
Als Output liefert Mathematica den Wert $\phi$ = 1,55324. Dies ist in recht guter Näherung $\pi/2$, der Stab ist nach der Fallzeit von etwa T = $82 \cdot \Delta$t = 82/100 s also auf dem Boden angelangt. Das Programm scheint somit zu funktionieren.
In den weiteren Aufgaben und Experimenten ist man daran interessiert, wie lange die Fallzeit T ist. Für das hier verwendete Verfahren bedeutet das also, wie viele Schritte benötigt werden, bis ein Winkel von etwa $\pi/2$ erreicht ist, sodass der Stab auf den Boden trifft. Eine Liste liefert zunächst die $\phi$ Werte für verschiedene Anzahlen an durchgeführten Zeitschritten:
liste1[n_,x0_,h_,l_]:= Table[phineu[m,x0,h,l],{m,1,n,1}]
Die nachfolgende Funktion, die ich “Winkel” genannt habe, filtert das größte Element der obigen Liste, das noch kleiner als $\pi/2$ ist:
winkel[n_,x0_,h_,l_]:=Max[Select[liste1[n,x0,h,l], # <= \[Pi]/2 &]]
Anschließend kann die Position dieses größten Elements in der Liste bestimmt werden, was gleichbedeutend mit der Anzahl an durchgeführten Zeitschritten ist:
schritte[n_,x0_,h_,l_]:=First[First[Position[liste1[n,x0,h,l],winkel[n,x0,h,l]]]]
So beispielsweise für die obigen Parameter von l = 1,45 und $\phi_0$ = 0,25 rad sowie einem Zeitschritt von $\Delta$t = 1/100 s = 10 ms:
schritte[100,0.25,1/100,1.45]
Als Output liefert Mathematica den Wert 82. Dies entspricht dann einer Fallzeit von T = $82 \cdot \Delta t$ = 82/100 s = 0,82 s, was sich auch mit der Abbildung 3 aus der Versuchsanleitung bestätigen lässt. Das Programm scheint zu funktionieren und es können nun insbesondere die Anfangswinkel $\phi_0$ sowie die Stablänge l, aber auch die Schrittweite $\Delta$ t =:h des Zeitschrittverfahrens variiert werden.
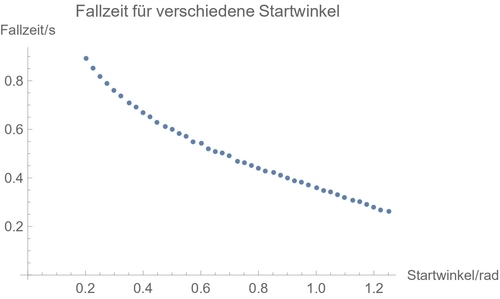
Über einen Listplot lässt sich sogar eine Abbildung ähnlich der Abbildung 3 aus der Versuchsanleitung erzeugen:
ListPlot[Table[{x0, (1/100)*schritte[100,x0,1/100,1.45]}, {x0,0.2,1.25,0.025}],
PlotLabel-> "Fallzeit für verschiedene Startwinkel", AxesLabel->{"Startwinkel/rad","Fallzeit/s"}]
Mathematica liefert als Output die folgende Graphik, die so wie in Abbildung 3 der Versuchsanleitung aussieht:
2.) Numerische Lösung mit NDSolve
Aus dem ersten Semester MMdP ist bekannt, dass sich im NDSolve - Befehl von Mathematica (numerische Lösung von DGL's) bereits ein “eingebautes” Zeitschrittverfahren befindet. Dies lässt sich nutzen, indem die Methode “ExplicitEuler” angegeben wird. Über “StartingStepSize” kann dann die Größe der Zeitschritte festgelegt werden:
lösung[a_,b_,c_] := NDSolve[{phi''[t] == (3*9.81/(2*c))*Sin[phi[t]], phi[0] == a, phi'[0] == 0},
phi[t], {t, 0, 100},
Method -> "ExplicitEuler", "StartingStepSize" -> b]
Um mit der Lösung weiterarbeiten zu können, wird die Funktion “phi” definiert, die bei einem Anfangswinkel von $\phi_0$ =:a, einer Schrittweite der Zeitschritte von $\Delta$t =: b sowie einer Stablänge von l =: c zu einer Zeit t =: $\tau$ die numerisch genäherte Lösung ausgibt:
phi[a_, b_,c_,tau_]:= First[(phi[t]/.lösung[a,b,c])/.t-> tau]
So bspw. für $\phi_0$ = 0,25 rad und $\Delta$t = 1/100 s = 10 ms und l = 1,45 m zu einer Zeit von t = 0,82 s:
phi[0.25,1/100,1.45,0.82]
Als Output liefert Mathematica den Wert $\phi$ = 1,55324. Man sieht also, dass in guter Näherung der Winkel $\phi = \pi$/2 rad erreicht ist, was bedeutet, dass der Stab auf den Boden trifft. Damit ist in etwa t = 0,82 s =: T die Fallzeit des Stabes. Dies lässt sich mit Abbildung 3 der Versuchsanleitung verifizieren, denn auch dort lässt sich für die entsprechenden Parameter von $\phi_0$, l und $\Delta$t eine Fallzeit von etwa T = 0,82 s ablesen. Das Programm scheint zu funktionieren. Es ergibt sich bei den gleichen Parameterwerten sogar der gleiche Wert für den Winkel, wie er eben bei der “händischen Implementierung ohne NDSolve” ermittelt wurde. Mathematica scheint also bei der Methode “EulerStep” tatsächlich einen sehr ähnlichen Algorithmus zu dem von mir “händisch” implementierten Zeitschrittverfahren zu benutzen!
Obige Funktion “phi” lässt sich nun bei festen $\phi_0$, l und $\Delta$t nach der Fallzeit auflösen, da nach dieser Zeit stets $\phi = \pi$/2 gilt:
fallzeit[a_,b_,c_]:=t/.FindRoot[phi[a,b,c,t] == Pi/2,{t,0.1}]
Für die bereits genutzten Parameter von $\phi_0$ = 0,25 rad und $\Delta$t = 1/100 s = 10 ms als Schrittweite sowie l = 1,45 m ergibt sich:
fallzeit[0.25,1/100,1.45]
Mathematica liefert als Output T = 0.823999 ,was in sehr guter Nähe zu der bereits bekannten und erwartbare Fallzeit von T $\approx$ 0,82 s liegt, die sich auch an Abbildung 3 aus der Versuchsanleitung ablesen lässt.
Wenn $\Delta$t = 10 ms und l = 1,45 m festgehalten werden, so lässt sich über einen Listplot eine Graphik genau so wie in Abbildung 3 aus der Versuchsanleitung erzeugen, indem verschiedenen Anfangswinkeln $\phi_0$ die Fallzeiten zugeordnet werden. Das Programm scheint also zu funktionieren:
ListPlot[Table[{phi0,fallzeit[phi0,1/100,1.45]},{phi0,0.2,1.25,0.025}],
PlotLabel->"Fallzeit für unterschiedliche Anfangswinkel",
AxesLabel->{"Startwinkel/rad", "Fallzeit/s"}]
Mathematica liefert als Output die folgende Graphik, die so wie in Abbildung 3 der Versuchsanleitung aussieht:
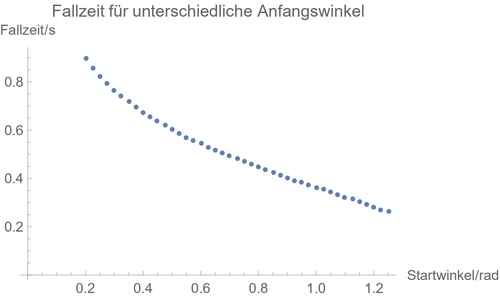
Mit Mathematica ergeben sich also zwei verschiedene Möglichkeiten für die numerische Lösung mit Zeitschrittverfahren, die beide auf entsprechende Fallzeiten sowie eine Graphik genau so wie in Abbildung 3 der Versuchsanleitung führen. Schlussendlich für die weitere Auswertung habe ich mich für die erste Möglichkeit entschieden, also das “händische Implementieren” ohne NDSolve. Der erste Grund dafür ist, dass ich zum einen nicht genau herausfinden konnte, ob die in Mathematica eingebautete Methode “ExplicitEuler” tatsächlich das in der Aufgabe vorgegebene Zeitschrittverfahren nutzt, oder doch eine leicht abgeänderte Variante. Der zweite Grund ist, dass mir das Arbeiten mit den Listen bzw. Punktepaaren bei der ersten Methode etwas einfacher gefallen ist.
Versuchsdurchführung/aufbau mit Bildern
Die Messung der Kippbewegung des Stabes habe ich mit zwei unterschiedlichen Stäben durchgeführt:
1.) Mit einem “echten Besenstiel” mit einer Länge von l = 1,505 m.

2.) Mit einem anderen, kürzeren Holzstab der Länge l = 1,223 m. Dieser ist dünner als ein herkömmlicher Besenstiel und wurd vmtl. als Rankhilfe für Gewächse genutzt.

Beide Stäbe sind massiv aus Holz und jeweils verglichen mit ihrer Länge dünn. Sie entsprechen beide also recht gut dem Modell eines “unendlich dünnen” Stabes, das u.a. bei der Herleitung der Differentialgleichung für den Winkel $\phi$ genutzt wurde (denn dort hat man ja das Trägheitsmoment eines solchen “unendlich dünnen” Stabes genutzt). Darüber hinaus sind beide Stäbe nicht verbogen, sodass es in dieser Hinsicht zu keiner Beeinflussung der Messungen kommen sollte. Die beiden Längen der Stäbe liegen mit knapp 30 cm so weit auseinander, dass sich unterschiedliche Messreihen gut aufnhemen lassen sollten. Hier ein Größenvergleich:

Nun zur eigentlichen Durchführung der Messungen, zuerst für den längeren Stiel. Es ist die Fallzeit des Stabes in Abhängigkeit von dem Anfangswinkel $\phi_0$ zu messen. Zuerst galt es deshalb, den Stab so fallenzulassen, dass er eine möglichst “reine” Fallbewegung ausführt, insbesondere ohne zu rutschen. Zunächst einmal hat der längere Besenstiel aufgrund seiner Bauform dieses Rutschen schon ein wenig eingedämmt, denn er besitzt an einer Seite ein leicht angespitztes Ende:

Auf dem Vinylboden bei mir kam es dennoch zu einer recht starken Rutschbewegung beim Fallen. Aus diesem Grund habe ein Stück “Malervlies” am Boden festgeklebt. Dieser hat eine besonders raue und rutschfeste Oberfläche:

Den Besenstiel habe ich dann mittig auf dem Vliesstück platziert und es gab beim Fallen praktisch keine Rutschbewegung mehr. Um den Boden mit den fallenden Stäben nicht zu verkratzen, habe ich den Punkt des Aufpralls des Besenstiels mit einem Textilstück abgefedert:

Messwerttabellen
Für die unterschiedlichen Anfangswinkel habe ich jeweils fünf mal gemessen.
Die Anfangswinkel $\phi_0$ habe ich jeweils in Abständen von 10° verändert, um auch wirklich verschiedene Winkel gut einstellen zu können.
Bis hoch zu 70° als Anfangswinkel, ab dann waren höhere Winkel nicht mehr gut einstellbar und es hätte eine sehr große Streuung der Messwerte gegeben.
Behandlung entsprechender Messunsicherheiten im Versuchsbericht.
1.) Messreihe mit dem längeren Stiel (l = 1,505 m)
| Messung | $\phi_0$ = 0°= 0 rad | $\phi_0$ = 10°$\approx$ 0,175 rad | $\phi_0$ = 20°$\approx$ 0,349 rad | $\phi_0$ = 30°$\approx$ 0,524 rad | $\phi_0$ = 40°$\approx$ 0,698 rad | $\phi_0$ = 50°$\approx$ 0,873 rad | $\phi_0$ = 60°$\approx$ 1,047 rad | $\phi_0$ = 70°$\approx$ 1,222 rad |
|---|---|---|---|---|---|---|---|---|
| 1 | 1,415 | 0,989 | 0,693 | 0,619 | 0,533 | 0,430 | 0,352 | 0,312 |
| 2 | 1,373 | 1,045 | 0,789 | 0,636 | 0,497 | 0,420 | 0,341 | 0,255 |
| 3 | 1,327 | 1,040 | 0,745 | 0,633 | 0,516 | 0,416 | 0,334 | 0,308 |
| 4 | 1,427 | 1,021 | 0,718 | 0,621 | 0,525 | 0,436 | 0,349 | 0,292 |
| 5 | 1,427 | 1,006 | 0,759 | 0,610 | 0,537 | 0,401 | 0,331 | 0,291 |
2.) Messreihe mit dem kürzeren Stiel (l = 1,223 m)
| Messung | $\phi_0$ = 0°= 0 rad | $\phi_0$ = 10°$\approx$ 0,175 rad | $\phi_0$ = 20°$\approx$ 0,349 rad | $\phi_0$ = 30°$\approx$ 0,524 rad | $\phi_0$ = 40°$\approx$ 0,698 rad | $\phi_0$ = 50°$\approx$ 0,873 rad | $\phi_0$ = 60°$\approx$ 1,047 rad | $\phi_0$ = 70°$\approx$ 1,222 rad |
|---|---|---|---|---|---|---|---|---|
| 1 | 1,198 | 0,938 | 0,706 | 0,523 | 0,487 | 0,402 | 0,313 | 0,221 |
| 2 | 1,314 | 0,898 | 0,711 | 0,566 | 0,513 | 0,406 | 0,290 | 0,217 |
| 3 | 1,198 | 0,894 | 0,735 | 0,552 | 0,476 | 0,377 | 0,302 | 0,228 |
| 4 | 1,222 | 1,001 | 0,685 | 0,559 | 0,498 | 0,412 | 0,338 | 0,244 |
| 5 | 1,210 | 0,989 | 0,698 | 0,539 | 0,491 | 0,413 | 0,323 | 0,230 |
Syntax und Funktionen im Wiki
Hier noch Links zu
- Hier im Wiki gibt es Hinweise für die Formatierung ihres Versuchsberichts mit Latex. Den Versuchsbericht geben Sie dann im Ilias ab.
- Für eine Tabelle mit Ihren Messwerten gibt es im oben im Editfenster des Wikis eine Hilfsfunktion. Sie versteckt sich hinter einem Knopf der so aussieht, wie ein hellblauer Taschenrechner.
- Außerdem ist es möglich einen Link zum Download des präsentierten Programm-Codes anzuzeigen. Dazu geben Sie in dem einleitenden code-Tag einen Dateinamen an. Der Download bezieht sich unmittelbar auf das Im Editor eingetragene Programmstück. Ein getrennter Upload ist nicht nötig.
- Ein Bild laden Sie ins Wiki, indem Sie im Editor in der Knopfleiste auf den kleinen Bildrahmen klicken. In einem neuen Fenster öffnet sich ein Dialog mit einem Dateibaum. Dort navigieren Sie zu “Ihrer” Baustelle (a_mechanik:kippender_besenstiel:gruppenseiten:gruppe352). Anschließend nutzen Sie den Dialog auf der rechten Seite, um Ihr Bild hochzuladen. Mit einem Klick auf die Zeile ihres Bildes erzeugen Sie im Hauptfenster einen Befehl, der das Bild lädt. Im einfachsten Fall landet ein Bild direkt an der Stelle im Text, an der Sie es eingefügt haben (Siehe de:wiki:syntax#bilder_und_andere_dateien. Hier gibt es einen Überblick, was sonst noch möglich ist.