meta data for this page
This is an old revision of the document!
Drehschwingung - Gruppe 342
Aufstellen der Bewegungsgleichung
Wir betrachten beim Drehpendel die Kraft, die auf ein Objekt beim Drehen um die Aufhängungsachse wirkt. Diese übersetzt sich mittels des Trägheitswiderstandes in eine Winkelbeschleunigung
$I \ddot{\phi} = D = - D_R \phi $
Dabei bezeichnen wir: $I$ den Trägheitsmoment, $D$ in $[Nm]$ Drehmoment, $D_R$ in $[Nm/rad]$ Winkelrichtgröße und $\phi$ in $[rad]$ Winkelauslenkung der Aufhängung. $[rad] = 1$ gibt hier nur an, dass es sich um einen Winkel im Bogenmaß handelt.
Insbesondere ist die Winkelrichtgröße gegeben als
$D_R = \frac{\pi}{2} \frac{G r^4}{L}$
mit $r$ Radius der Aufhängung, $G$ Torsionsmodul (Materialkonstante) und $L$ Länge des Drahtes.
Wir sehen also an $D_R \propto r^4$, dass eine kleine Erhöhung im Drahtradius das Drehmoment stark beeinflusst. Verdoppeln wir die Dicke erhalten wir also $D_R' = 2^4 D_R = 16 D_R$ also eine Ver-16-fachung des Drehmoments.
Lösung der Bewegungsgleichung
Wir kennen die Basislösung $\phi(t) = A \sin{\omega t} + B \cos{\omega t}$ mit $\dot{\phi}(t) = A \omega \cos{\omega t} - B \omega \sin{\omega t}$ für die DGL. Betrachten wir nun das Auslenken des Pendels um $\phi(0) = \phi_0$ und das Loslassen ohne Anfangsgeschwindigkeit $\dot{\phi}(0) = \dot{\phi}_0$ erhalten wir
$\dot{\phi}(0) = A \omega \cos{0} - B \omega \sin{0} = A \omega = 0 \rightarrow A = 0 $
$\phi_0 = B \cos{0} = \phi_0 \rightarrow B = \phi_0$
Wir erhalten also $\phi(t) = \phi_0 \cos{\omega t}$ als Bahnkurve. Einsetzen in die DGL
$I \ddot{\phi} = D = - D_R \longleftrightarrow I \phi_0 (-\omega^2) \cos{\omega t} = - D_R \phi_0 \cos{\omega t} \longrightarrow \omega^2 = \frac{D_R}{I}$.
Damit können wir die Periodendauer angeben
$ T_{Periode} = \frac{1}{f} = \frac{1}{2 \pi \omega} = \frac{1}{2 \pi} \sqrt{\frac{I}{D_R}}$
Unter der Annahme eines harmonischen Potentials können wir die Periodendauer $T \neq T(\phi_0)$ als konstant ansehen. Somit ist $T_{Schwingungsdauer} = T_{Periode} := T$
$ T := T(L) = \frac{1}{2 \pi} \sqrt{\frac{2 I L}{\pi G r^4}} = \frac{1}{2 \pi r^2} \sqrt{\frac{2 I}{\pi G}} \cdot \sqrt{L}$
Für $T^2$ finden wir einen linearen Zusammenhang:
$ T^2 = \frac{I}{2 \pi^3 G r^4} \cdot L $
Durchführung
Wir hängen also starre Körper verschiedener Geometrien an unterschiedlichen Aufhängungen auf. Nun lenken wir die Körper um einen Anfangswinkel $\phi_0$ aus und lassen sie ohne Anfangsgeschwindigkeit los. Nun messen wir zur Verbesserung der Genauigkeit die Zeit $T_n$ über $n$ Perioden. Durch das mitteln verkleinert sich unsere Messunsicherheit in der Zeit.
Abhängig von der Dämpfung Aufhängung, dem Trägheitsmoment des Körpers und dem Torsionsmodul $G$ wählen wir $\phi_0$ und $n$ sinnvoll. Der Schnürsenkel dämpft hier zum Beispiel stark, hat jedoch eine sehr geringe rücktreibende Kraft sodass wir $n$ klein und $\phi_0$ groß wählen.
Wir fangen damit an, das Torsionsmodul $G$ unter Bekanntheit des Trägheitsmoments $I$ des Stabes zu bestimmen. Dies erlaubt uns, im späteren Teil des Versuches Trägheitsmomente $I$ unbekannter Körper zu bestimmen. Wir errechen auch hier ein theoretisches Trägheitsmoment und vergleichen.
Energiebetrachtung
Wir interessieren uns für eine infinitesimale Winkeländerung $d\phi$. Die Arbeit $W$ entspricht dabei
$ W = \int D d\phi \longrightarrow \frac{dW}{d\phi} = \frac{d}{d\phi}\int D d\phi = D $
Umstellen liefert also
$dW = D \cdot d\phi$
Betrachten wir die Rotationsenenergie $E = \frac{1}{2} I (\frac{d\phi}{dt})^2$
$\frac{dE}{dt} = \frac{dE}{d\phi}\frac{d\phi}{dt} = I \frac{d^2\phi}{dt^2} \frac{d\phi}{dt} \longleftrightarrow dE = I \ddot{\phi} \cdot d\phi $
Gleichsetzen von $E = W$ liefert schließlich mit $D = - D_R \phi$
$ I \ddot{\phi} = D = - D_R \phi $
Wir erhalten unsere DGL also auch mittels einer Energiebetrachtung.
Steiner'scher Satz
Unter Kenntnis des Trägheitsmomentes starrer Körper mit Gesamtmasse $M$ um eine feste Achse durch den Schwerpunkt $I_S$ erlaubt der Steiner'sche Satz die Berechnung des Trägheitsmomentes $I'$ um eine parrelel um $d$ verschobene Achse:
$I' = I_S + M d^2 $
Zur Herleitung benötigen wir nur die Vektoraddition $\vec{x} = \vec{x'} + \vec{\delta x}$ und die Definition des Schwerpunktes als Punkt, an dem die Integrale $\int_V \rho \cdot r_i = 0$ für $r = (x,y,z)$ verschwinden.
Wir betrachten also das Trägheitsmoment I' entlang einer Achse $\vec{n}$ und setzen den Urspung des Koordinatensystem in den Schwerpunkt und die z-Achse parallel zur Drehachse. Damit gilt für den Abstand r eines Punktes zur Drehachse
$ r^2 = (\delta x)^2 + (\delta y)^2$
Setzen wir ein in die Definition des Trägheitsmomentes mit Massendichte $\rho$
$I' = \int_V \rho (\delta x)^2 + (\delta y)^2$
$I' = \int_V \rho (x - x')^2 + (y-y')^2$
Terme aufdröseln:
$I' = \int_V \rho x^2 + y^2 + \int_V \rho x'^2 + y'^2 $
$I' = I_S + (x'^2 + y'^2) \cdot \int_V \rho - 2 y' \int_V \rho x - 2 x' \int_V \rho y$
$I' = I_S + M d^2 $
mit $d = (x'^2 + y'^2)$ ist der Steiner'sche Satz.
Berechnung der Trägheitsmomente mittels der Geometrie
Wir berechnen die Trägheitsmomente $I$ nach der Formel
$ I=\int _{V}{\vec {r}}_{\perp }\!^{2}\rho ({\vec {r}})\mathrm {d} V $
wobei wir die Massendichte $\rho({\vec {r}}) = const. $ annehmen.
Die hohe Unsicherheit ist damit zu erklären, dass wir keine Küchenwaage besitzen. Wir bauen uns also folgende Apparatur auf:
Zuerst messen wir das Gewicht gegen die Füllhöhe der Flasche mit $u(\delta m) = 0,02 kg$. Wir rütteln, um den Einfluss der Haftreibung zu minimieren. Nun messen wir das Nullgewicht $m_0 = 0,07 \pm 0,01 kg$ der Flasche mittels einer Kippwaage. Dazu stellen wir nacheinander leere und volle Shotgläser auf die Waage auf gegenüberliegende Seiten. Mittels der Füllhöhe der Shotgläser und der Dichte von Wasser $\rho \approx 1 kg/m^3$ erhalten wir so also das Gewicht, was wir im folgenden als Summe über $m = \delta m + m_0$ schreiben werden. Die Unsicherheit ist damit $u(m) = 0,03 kg$.
Dünner Metallstab
Aufgrund der Prorportion $r \ll L$ können wir eine Vereinfachung für die Rotation quer durch den Schwerpunkt benutzen. Wir führen eine 1-D Integration entlang des Stabes durch mit 1-D Massendichte $\rho_0 = M/l$:
$I = \rho_0 \int_0^{l/2} r_{\perp }\!^{2} = \rho_0 \frac{1}{3} (\frac{l}{2})^3 = \frac{l}{M} \frac{1}{12} l^3 = \frac{1}{12} M l^2 $
Die exakte Formel auf dem Arbeitsblatt erhalten wir durch 3-D Integration. Für $r \ll L$ fällt der vordere Term aber nicht ins Gewicht.
Für den dünnen Metallstab messen wir
$ l = 0.12 \pm 10^{-3} m, M = 0.04 \pm 0.01 kg $
Nach Gauß'scher Fehlerfortpflanzung gilt:
${u_{I}} = {\sqrt {\left({\frac {\partial I}{\partial M}}\cdot u_{M}\right)^{2}+\left({\frac {\partial I}{\partial l}}\cdot u_{l}\right)^{2}}} $
${u_{I}} = \frac{1}{12} {\sqrt {\left({l^2}\cdot u_{M}\right)^{2}+\left({2Ml}\cdot u_{l}\right)^{2}}}$
${u_{I}} \approx 1,2 \cdot 10^{-5}\ kg\ m^2$
ergibt uns
$I_{Stab} = (4,8 \pm 1,2) \cdot 10^{-5}\ kg\ m^2$
Topfdeckel
Für die Topfdeckel nähern wir die Geometrie als homogonen Zylinder. Wir integrieren also in 2-D Polarkoordinaten mit 2-D Massendichte $\rho_0 = \frac{M}{\pi R^2}$
$ I = \rho_0 \int_0^{2\pi} d\phi \int_0^R r\ dr\ r^2 = \frac{M}{\pi R^2} \ 2\pi\ \frac{1}{4} R^4 = \frac{1}{2}M R^2$
Wir messen die Topfdeckel ab
$R_{1} = d_1/2 = (0.105 \pm 0.0025) m $
$ M_1 = (0.07 + 0.65) \pm 0.03 kg = (0.72 \pm 0.03) kg $
$ R_2 = d_2/2 = (0.085 \pm 0.0025) m$
$M_2 = (0.07 + 0.05) \pm 0.03 kg = (0.12 \pm 0.03) kg$
Die Unsicherheit erhalten wir beinahe analog
${u_{I}} = {\sqrt {\left({\frac {\partial I}{\partial M}}\cdot u_{M}\right)^{2}+\left({\frac {\partial I}{\partial l}}\cdot u_{l}\right)^{2}}} $
${u_{I}} = \frac{1}{2} {\sqrt {\left({R^2}\cdot u_{M}\right)^{2}+\left({2MR}\cdot u_{R}\right)^{2}}}$
${u_{I_1}} \approx 4,18 \cdot 10^{-5}\ kg\ m^2$
${u_{I_2}} \approx 1,86 \cdot 10^{-5}\ kg\ m^2$
Damit ergeben sich die Trägheitsmomente
$ I_1 = (3,97\pm 0,04) \cdot 10^{-3} \ kg\ m^2$
$ I_2 = (0,43\pm 0,02) \cdot 10^{-3} \ kg\ m^2$
Der Fehler ist hier aber eigentlich deutlich größer, da wir von einer homogenen Masseverteilung ausgehen, was offensichtlich nicht der Fall ist.
Messung 1 - Stab an Saite dünn ($r= 0.4 \pm 0.1$)
Anfangsbedingungen:
$\phi_0 = \pi,$ $\dot{\phi}_0 = 0$
Unsicherheiten:
$ u(L) = 0,03m, u(T_{10}) = 0,5s$
| Höhe $L/m$ | Periodendauer $T_{10}/s$ |
|---|---|
| 0,56 | 17,5 |
| 0,42 | 15,9 |
| 0,35 | 15,6 |
| 0,29 | 12,9 |
| 0,24 | 12,58 |
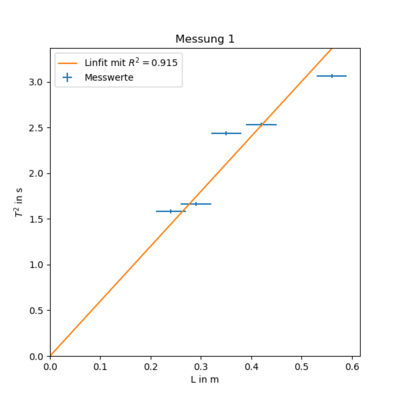
$ T(L)^2 = (4.8 \pm 0.8)\frac{s^2}{m} \cdot L + (0.5 \pm 0.3)s^2 $
Aus der Theorie erwarten wir eine Steigung die sich aus $(4.8 \pm 0.8)\frac{s^2}{m} = \frac{I}{2 \pi^3 G r^4}$ zusammensetzt. Außerdem kennen wir schon $ I = (4,8 \pm 1,2) \cdot 10^{-5}\ kg\ m^2 $ und $ r = (0.4 \pm 0.1)mm \Longrightarrow r^4 = (0.0 \pm 0.4)mm $. Nach Umstellen ergibt sich:
$ G = \frac{(4,8 \pm 1,2) \cdot 10^{-5}\ kg\ m^2}{2 \pi^3 (4.8 \pm 0.8)\frac{s^2}{m} (0.0 \pm 0.4)mm} = (0 \pm 110) 10^6 \frac{kg}{s^2 m}$
Da der relative Fehler viel zu groß ist und der $T^2$-Achsenabschnitt auch ziemlich groß ist, ist dieser Wert für weitere Berechnungen nicht emphelenswert.
Messung 2 - Stab an Saite dick ($r = (1 \pm 0.1)mm$)
Anfangsbedingungen:
$\phi_0 = \pi, \dot{\phi}_0 = 0$
Unsicherheiten:
$ u(L) = 0,03m,$ $u(T_{10}) = 0,5s$
| Höhe $L/m$ | Periodendauer $T_{10}/s$ |
|---|---|
| 0.62 | 16.32 |
| 0.53 | 13.44 |
| 0.47 | 12.68 |
| 0.35 | 11.49 |
| 0.23 | 9.47 |
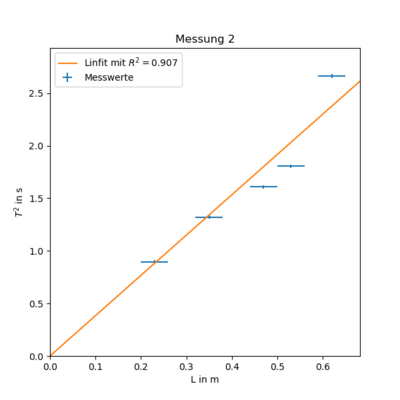
$ T(L)^2 = (4.1 \pm 0.8)\frac{s^2}{m} \cdot L + (-0.1 \pm 0.3)s^2 $
Aus der Theorie erwarten wir eine Steigung die sich aus $(4.1 \pm 0.8)\frac{s^2}{m} = \frac{I}{2 \pi^3 G r^4}$ zusammensetzt. Außerdem kennen wir schon $ I = (4,8 \pm 1,2) \cdot 10^{-5}\ kg\ m^2 $ und $ r = (1.0 \pm 0.1)mm \Longrightarrow r^4 = (1.0 \pm 0.4)mm^4 $. Nach Umstellen ergibt sich:
$ G = \frac{(4,8 \pm 1,2) \cdot 10^{-5}\ kg\ m^2}{2 \pi^3 (4.1 \pm 0.8)\frac{s^2}{m} (1 \pm 0.4)mm^4} = (190 \pm 90) 10^3 \frac{kg}{s^2 m} $
Diese Berechnung ist im Vergleich zur ersten deutlich plausibler.
Messung 3 - Stab an Schnürsenkel ($r = (3 \pm 1)mm$)
Anfangsbedingungen:
$\phi_0 = 4 \cdot \pi, \dot{\phi}_0 = 0$
Unsicherheiten:
$ u(L) = 0,03m, u(T_{2}) = 0,5s$
Die Dämpfung ist hier groß. Deshalb messen wir 2 Perioden $T_2$ statt 10 Perioden $T_{10}$.
| Höhe $L/m$ | Periodendauer $T_{2}/s$ |
|---|---|
| 0,48 | 26,86 |
| 0,18 | 19,37 |
| 0,10 | 13,58 |
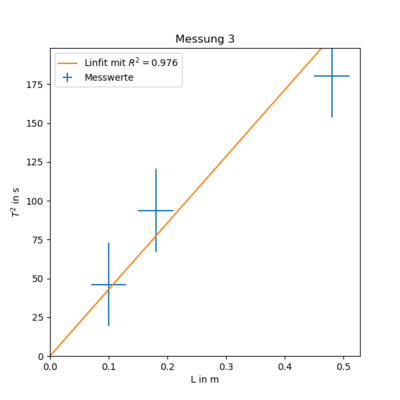
$ T(L)^2 = (340 \pm 50)\frac{s^2}{m} \cdot L + (22 \pm 16)s^2 $
Aus der Theorie erwarten wir eine Steigung die sich aus $(340 \pm 50)\frac{s^2}{m} = \frac{I}{2 \pi^3 G r^4}$ zusammensetzt. Außerdem kennen wir schon $ I = (4,8 \pm 1,2) \cdot 10^{-5}\ kg\ m^2 $ und $ r = (1.0 \pm 0.1)mm \Longrightarrow r^4 = (81 \pm 4)mm^4 $. Nach Umstellen ergibt sich:
$ G = \frac{(4,8 \pm 1,2) \cdot 10^{-5}\ kg\ m^2}{2 \pi^3 (340 \pm 50)\frac{s^2}{m} (81 \pm 4)mm^4} = (2.3 \pm 0.7) 10^3 \frac{kg}{s^2 m}$
Diese Berechnung scheitert an der Annahme eines harmonischen Potentials.
Messung 4 - Topfdeckel 1 an Saite dick
Durchmesser $ d = (0.210 \pm 0.005) m $
Masse $ m = (0.07 + 0.65) kg $
Anfangsbedingungen:
$\phi_0 = \pi, \dot{\phi}_0 = 0$
Unsicherheiten:
$ u(L) = 0,03m, u(T_{3}) = 0,5s, u(m) = 0.03 kg$
| Höhe $L/m$ | Periodendauer $T_{3}/s$ |
|---|---|
| 0.56 | 38.88 |
| 0.29 | 27.11 |
| 0.17 | 20.57 |
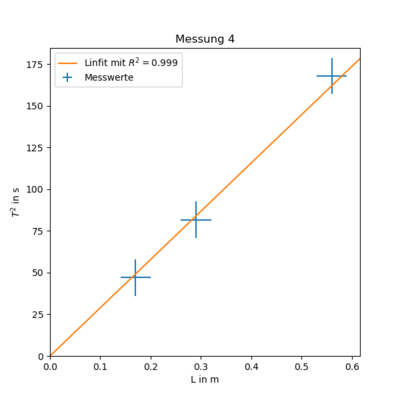
$ T(L)^2 = (311 \pm 7)\frac{s^2}{m} \cdot L + (-7 \pm 3) $
Vergleicht man nun den Proportionalitätfaktor mit dem aus Messung 2 erhält man $ I_{Topf1}= \frac{(311 \pm 7)\frac{s^2}{m}}{(4.1 \pm 0.8)\frac{s^2}{m}} \cdot (4,8 \pm 1,2) \cdot 10^{-5}\ kg\ m^2 = (3.7 \pm 1.1) 10^{-3} \ kg\ m^2 $
Messung 5 - Topfdeckel 2 an Saite dick
Durchmesser $ d = (0.170 \pm 0.005) m $
Masse $ m = (0.07 + 0.05) kg $
Anfangsbedingungen:
$\phi_0 = \pi, \dot{\phi}_0 = 0$
Unsicherheiten:
$ u(L) = 0,03m, u(T_{5}) = 0,5s, u(m) = 0.03 kg $
| Höhe $L/m$ | Periodendauer $T_{5}/s$ |
|---|---|
| 0.50 | 26.69 |
| 0.33 | 21.36 |
| 0.17 | 14.51 |
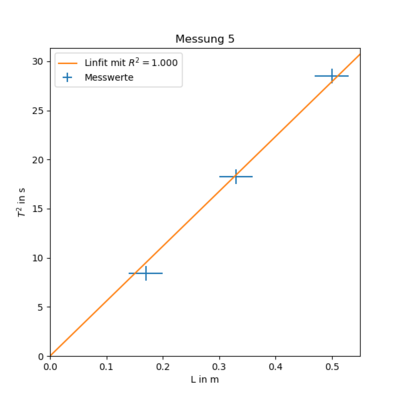
$ T(L)^2 = (60.8 \pm 0.3)\frac{s^2}{m} \cdot L + (-1.89 \pm 0.12)s^2 $
Vergleicht man nun den Proportionalitätfaktor mit dem aus Messung 2 erhält man $ I_{Topf_2}= \frac{(60.8 \pm 0.3)\frac{s^2}{m}}{(4.1 \pm 0.8)\frac{s^2}{m}} \cdot (4,8 \pm 1,2) \cdot 10^{-5}\ kg\ m^2 = (0.71 \pm 0.22) 10^{-3} \ kg\ m^2 $
Auswertung
Code zu den Plots
import numpy as np import matplotlib.pyplot as plt from scipy import stats ul = 0.03 ut = 0.5 mess1 = {'val': np.array([[0.56, 17.5], [0.42, 15.9], [0.35, 15.6], [0.29, 12.9], [0.24, 12.58]]), 'phi': np.pi, 'nt': 10} mess2 = {'val': np.array([[0.53, 13.44], [0.62, 16.32], [0.47, 12.68], [0.35, 11.49], [0.23, 9.47]]), 'phi': np.pi, 'nt': 10} mess3 = {'val': np.array([[0.48, 26.86], [0.18, 19.37], [0.1, 13.58]]), 'phi': 4 * np.pi, 'nt': 2} mess4 = {'val': np.array([[0.56, 38.88], [0.29, 27.11], [0.17, 20.57]]), 'phi': np.pi, 'nt': 3} mess5 = {'val': np.array([[0.50, 26.69], [0.33, 21.36], [0.17, 14.51]]), 'phi': np.pi, 'nt': 5} messes = [mess1, mess2, mess3, mess4, mess5] for j in range(len(messes)): mess = messes[j] vals = np.transpose(mess['val']) nt = mess['nt'] lengths = vals[0] l_max = max(lengths) l_mean = sum(lengths) / len(lengths) lens = np.linspace(0, 1.1 * l_max, num=50) times = [vals[1][i] / nt for i in range(len(vals[1]))] t_quad = [times[i] ** 2 for i in range(len(times))] tq_max = max(t_quad) tq_mean = sum(t_quad) / len(t_quad) sol = stats.linregress(lengths[:len(t_quad)], t_quad) fit = [sol.slope * l + sol.intercept for l in lens] dls = [l - l_mean for l in lengths] sdl = sum([abs(dl) for dl in dls]) / len(dls) dtqs = [tq - tq_mean for tq in t_quad] sdtq = sum([abs(dtq) for dtq in dtqs]) / len(dtqs) covltq = sum([dls[i] * dtqs[i] for i in range(len(dls))]) / (len(dls) - 1) corltq = covltq / (sdl * sdtq) print('(%.3f' % (round(sol.slope, 3)) + ' \pm ' + '%.3f' % (round(sol.stderr, 3)) + ') \cdot L + ' + '(%.3f' % ( round(sol.intercept, 3)) + ' \pm ' + '%.3f)' % (round(sol.intercept_stderr, 3))) fig = plt.figure(figsize=(6, 6)) ax = fig.add_subplot(111) ax.errorbar(lengths, [time ** 2 for time in times], linestyle='', marker='', xerr=ul, yerr=2 * tq_mean * ut / nt, label='Messwerte') ax.plot(lens, fit, linestyle='-', label='Linfit mit $R^2 =$' + "%.3f" % (round(sol.rvalue ** 2, 3))) ax.set_xlim(0, 1.1 * l_max) ax.set_ylim(0, 1.1 * tq_max) ax.set_title('Messung ' + str(j + 1)) ax.set_xlabel('L in m') ax.set_ylabel('$T^2$ in s') ax.legend() plt.savefig('Drehschwingung.Messung' + str(j + 1) + '.png') plt.show()


